RNN
시계열, 시퀀스(sequence) 데이터에 주로 적용되는 네트워크이다.
Sequence Data
- 소리, 문자열, 주가 등의 데이터를 시퀀스 데이터로 분류한다.
- 시계열(time series)데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터에 속한다.
- 스퀀스 데이터는 독립동등분포(i.i.d) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다.
Sequence Data handle
- 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 사용할 수 있다.
- $X_1$부터 $X_t$까지의 결합확률 분포를 베이즈 법칙을 통해 위와 같이 모델링할 수 있다.
Autoregressive Model(AR)
- 실제 시퀀스 데이터를 분석할 때 모든 과거의 정보들이 필요한 것은 아니다.
- 고정된 길이 $\tau$만큼의 시퀀스만 사용하는 모델을 Autoregressive Model(자기회귀 모델)이라고 한다.
- 혹은 위의 수식처럼 바로 이전 정보를 제외한 나머지 정보들을 $H_t$라는 잠재변수로 인코딩해서 활용하는 모델을 잠재 AR 모델이라고 한다.
- RNN은 잠재변수 $H_t$를 신경망을 통해 반복 사용하여 스퀀스 데이터의 패턴을 학습하는 모델이다.
RNN forward propagation
- 가장 기본적인 RNN 모형은 MLP와 유사하다.
- 위의 수식에서 $W^{(1)}, W^{(2)}$는 t에 따라 변하지 않는 가중치 행렬이다.
Backpropagation Through Time(BPTT)
- RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산된다.(BPTT)
- 잠재변수에 들어오는 Gradient는 다음 시점의 잠재변수로부터 들어오는 Gradient 벡터와 출력으로부터 들어오는 Gradient 벡터 두개가 들어온다. 이러한 Gradient 벡터를 입력과 이전 시점의 잠재변수로 전달하며 학습이 진행된다.
BPTT를 통한 RNN의 가중치 행렬의 미분은 아래와 같이 미분의 곱으로 이루어진 항이 계산된다.
$\partial_{W_{h}}h_t=\partial_{W_{h}}h_tf(x_t,h_{t-1},w_h)+\displaystyle\sum_{i=1}^{t-1}(\prod_{j=i+1}^t\partial_{h_{j-1}}f(x_j, h_{j-1},w_h)\partial_{w_h}f(x_i,h_{i-1},w_h)$
- 위의 식에서 $\prod_{j=i+1}^t\partial_{h_{j-1}}f(x_j, h_{j-1},w_h)$항은 가장 마지막 Gradient까지 누적해서 곱하는 연산이다. Gradient가 계속 누적되서 곱해지기 때문에 스퀀스 길이가 길어짐에 따라 매우 커지거나 매우 작아질 수 있다. (exploding, vanishing) → 학습이 불안정해진다.
truncated BPTT
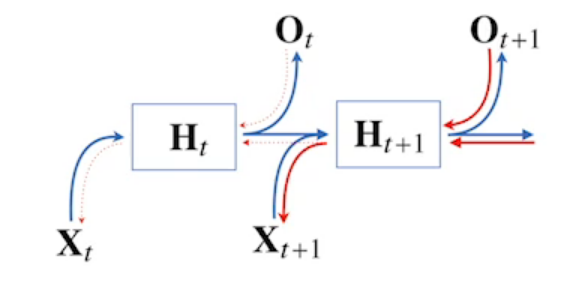
- 위에서 말한 BPTT의 문제점인 Gradient vanishing을 해결하기 위한 방법이 truncated BPTT이다.
- truncated BPTT는 Gradient를 전달할 때 모든 시점에 전달하지 않고 특정 시점에서 끊는 방법으로 Gradient를 나누어 전달하는 방식이다.
- 예를들어 위의 사진에서 $H_{t+1}$로부터 오는 Gradient를 받지 않고 $O_t$로부터 오는 Gradient만 $H_t$로 전달한다.
RNN 업데이트
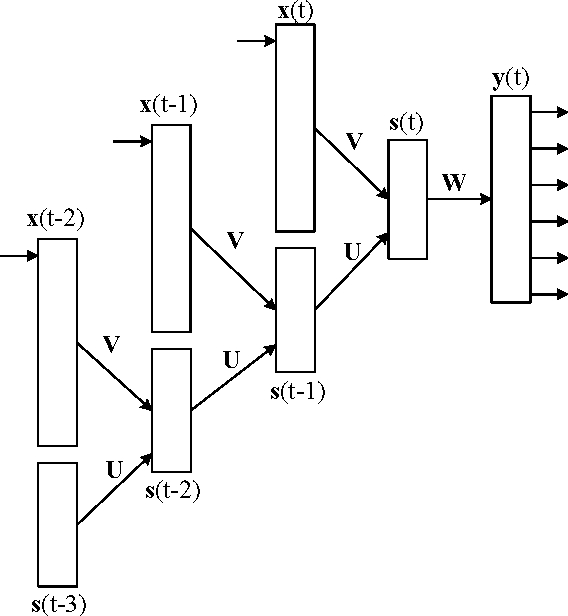
- 최종 출력을 하는 W의 가중치는 기존 BackParogation과 똑같이 계산할 수 있다.
- http://solarisailab.com/archives/1451
- TODO 위의 그림에서 V는 $W_X^{(1)}$, U는 $W_H^{(1)}$라고 생각이 드는데 위에서 교수님이 말씀하신것은 W들은 공통으로 사용된다고 하셨다. 하지만 위의 블로그를 보면 각 시점에 대한 V, U를 계산하는데 ………………………………..음….
Sequential Model
Markov model(first-order autoregressive model)

- 바로 직전의 과거만 현재에 영향을 끼친다고 가정한 모델이다.
- 결합분포를 쉽게 표현할 수 있다는 장점이 있다.
Latent autoregressive model
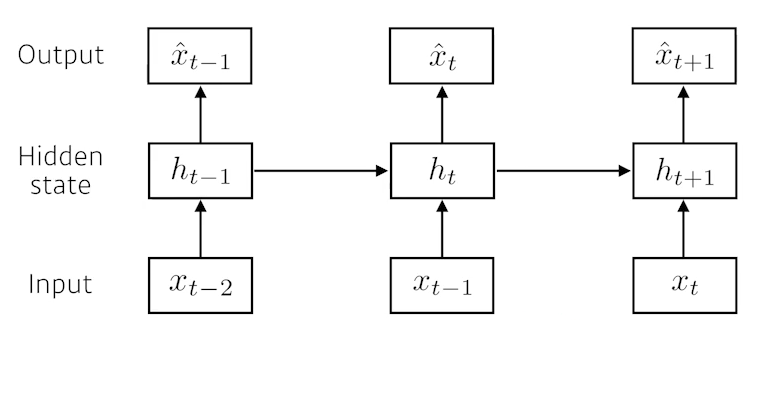
- 이전의 정보들을 요약한 h를 사용해 학습힌다.
Short term dependencies, Long term dependencies
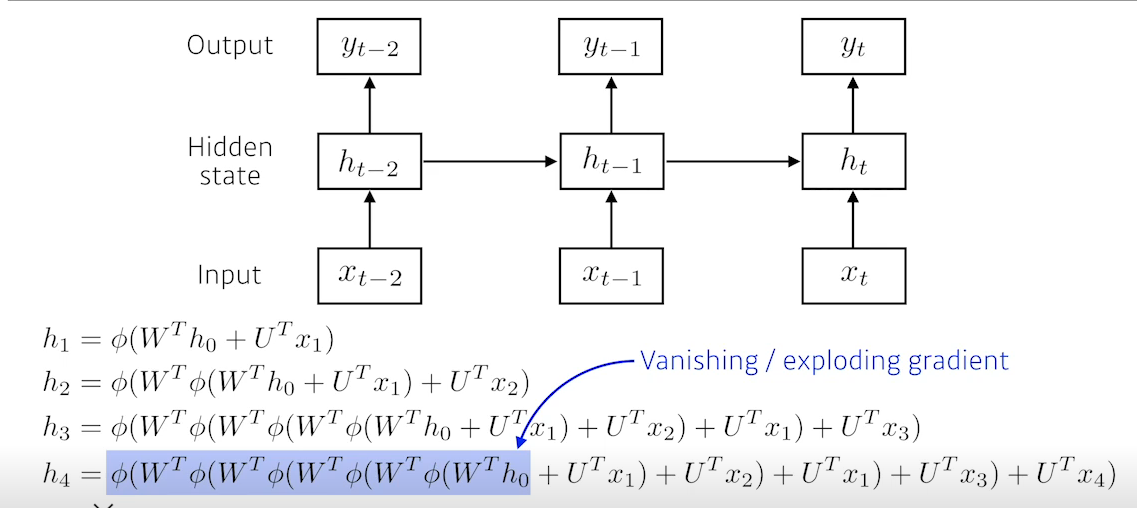
- 현재 시간기준 가까운 과거에 대한 정보는 잘 가질 수 있지만 계속 누적되는 방식이기 때문에 먼 과거의 데이터의 정보가 유실된다.
- 활성함수가 sigmoid나 tanh같은 경우 이전시간의 결과를 0 ~ 1사이로 계속 줄이는 과정이 중첩되어 Vanishing현상이 발생한다.
- 활성함수가 relu같은 경우 양수의 결과가 나오는것을 계속 곱하기 때문에 매우 큰 값이 되어 exploding gradient현상이 발생한다.
- 이러한 현상때문에 RNN할때 relu잘 안쓴다.
LSTM(Long Short Term Memory)
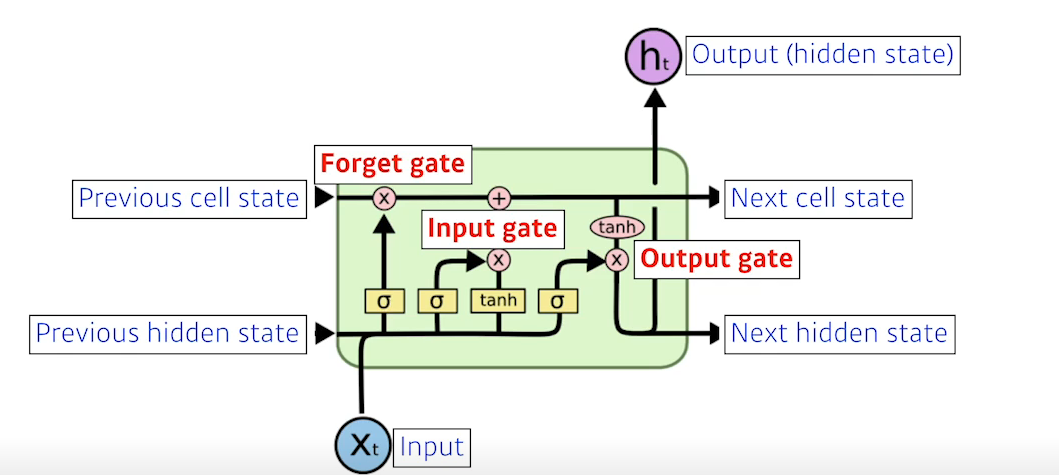
- LSTM를 그림으로 표현한 것이다. 위의 그림에서 연산기호가 들어가 있는 동그라미는 element wise operation을 의미한다.
Cell State
- LSTM의 핵심은 cell state이다.
- cell state란 이전 time stamp의 정보의 요약인데 gate를 통해 적절히 잊게하고 추가하여 긴 Sequential Data에서 이전의 데이터에 대한 정보를 유실하지 않도록 한다.
Forget gate
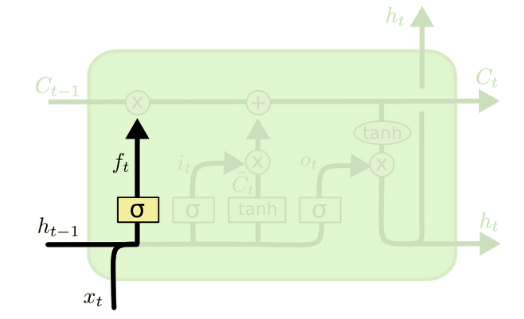
- Cell State에서 어떤 정보를 지울지 결정한다.
- Sigmoid연산을 통해 어떤 정보를 잊게할지 결정한다. (0 ~ 1값이 나아고, element wise mul을 하기 때문)
- $W_f$ 는 $[W_{fh},W_{fx}]$라고 생각하면 된다.
Input gate
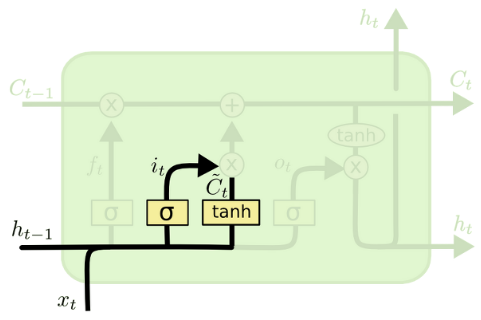
- 현재 정보를 기억하기 위한 게이트이다.
- 0~1값을 가지는 i와 -1~1값을 가지는 C를 사용해 선택된 정보와 기억할 정보의 양을 결정한다.
- 기억학 값을 C에 더함으로써 기억할 정보를 추가할 수 있다.
- $W_i$는 $[W_{ih},W_{ix}]$, $W_C$는 $[W_{Ch},W_{Cx}]$라고 생각하면 된다.
Output gate
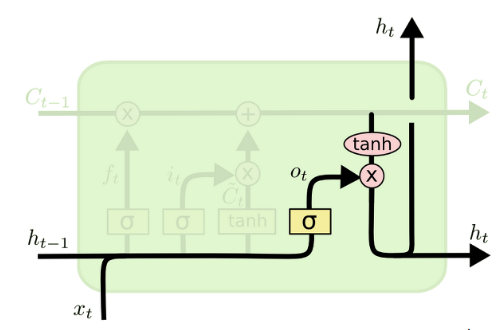
- Cell State의 Update를 모두 끝낸 뒤 Cell state를 바탕으로 output을 정한다.
GRU(Gated Recurrent Unit)
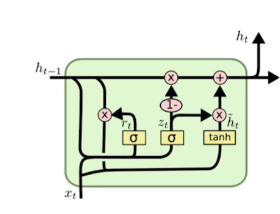
- GRU는 LSTM에서 Cell state를 제거한 모델이다.
- reset gate와 update gate 두개의 gate가 존재한다.
- hidden state가 곧 output이다.(Output gate가 필요없어짐)
- 많은 논문들에서 똑같은 Task에 대해서 LSTM보다 GRU를 활용했을 때 성능이 올라가는 경우가 꽤 있다고한다. (Parameter수가 적어서??)
Transformer
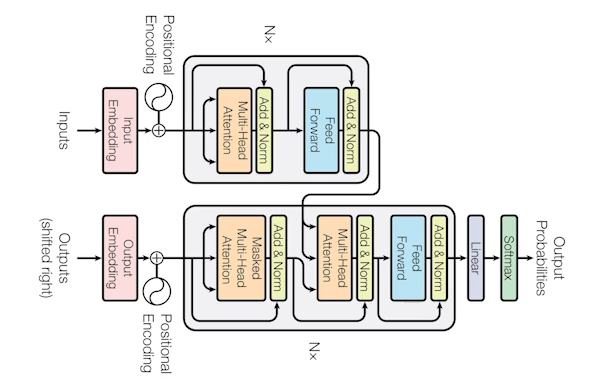
- RNN과 같은 재귀적인 구조가 아닌 attention이라는 구조를 활용하였다.
- 이 방법론은 sequential한 데이터를 처리하고 이 데이터를 Encoding하는 방법이기 때문에 단순히 기계어 번역뿐만 아니라 이미지 분류, Detection등 다양하게 사용될 수 있다.
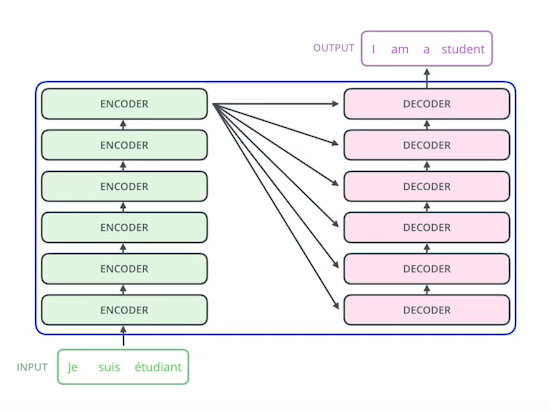
- 하나의 모델로 서로 다른 입력 sequence의 출력 크기, 도메인을 처리할 수 있다.
- RNN의 경우 input의 단어 개수만큼 재귀적으로 여러번 network가 동작됐다면 Transformer는 몇개의 단어가 들어오던지 한번에 모든 문장을 가지고 network를 동작시킨다. (generate할 때는 한 단어씩 만듬)
- N개의 단어를 한번에 처리할 수 있다 (Encoding)
- 동일한 구조를 가지지만 파라미터가 다르게 학습되는 인코더와 디코더가 쌓여있는 모델이다.
ENCODER
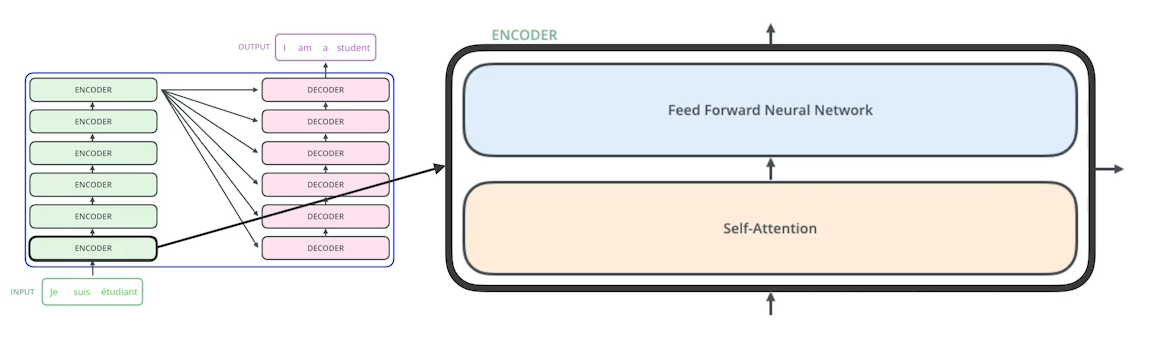
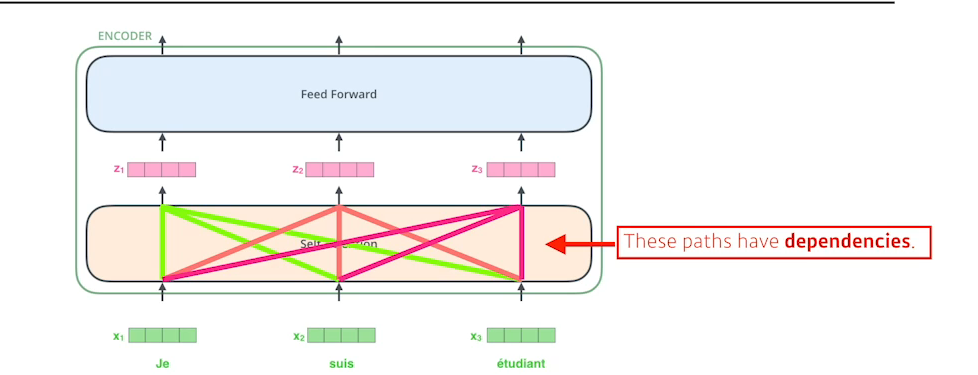
- Self Attention은 입력된 각 단어들을 Feature vector로 변환하는데 단순히 하나의 단어만 바라보고 만들지 않고 입력된 다른 단어들을 고려하여 생성한다.
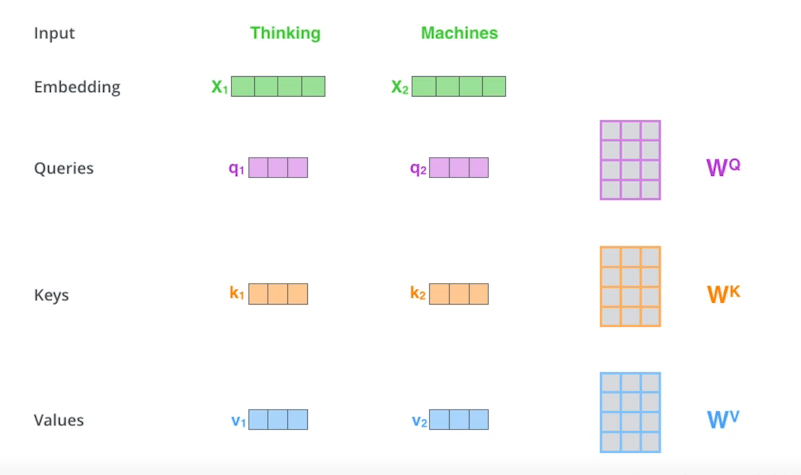
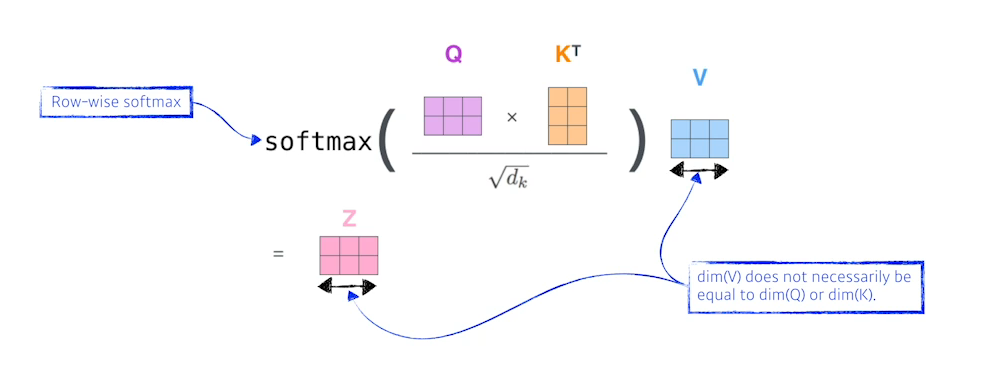
- 각 단어를 Encoding하는 과정은 해당단어(Embedding 된 벡터)를 각각의 NN를 통해서 Queries, Keys, Values 벡터를 구하고 현재 단어의 Query 벡터와 다른 모든 단어들의 Key 벡터를 내적해 현재 단어가 다른 벡터와 얼마나 관계가 있는지를 나타내는 Score 벡터를 구한다.
- 이러한 Score벡터를 Normalize해준다. → Key 벡터의 차원의 제곱근으로 score를 나눈다. (너무 커지지 않도록)
- Normalize한 score벡터에 Softmax를 취해준다.

- 그럼처럼 구해지고 이 값은 현재 단어와 다른 단어가 얼마나 interaction해야 하는지를 나타낸다.(Attention)
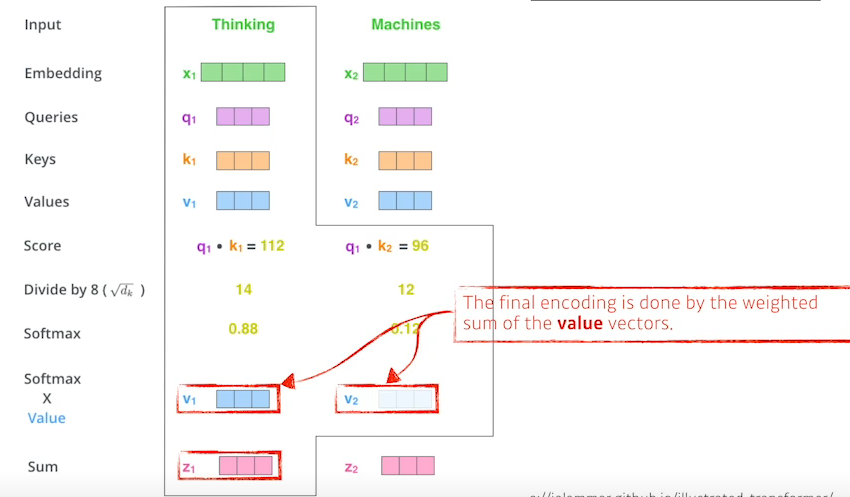
- Attention 값을 사용해 각 단어들의 Value 벡터를 weighted sum을해 인코딩을 완료한다.
Q, K, V
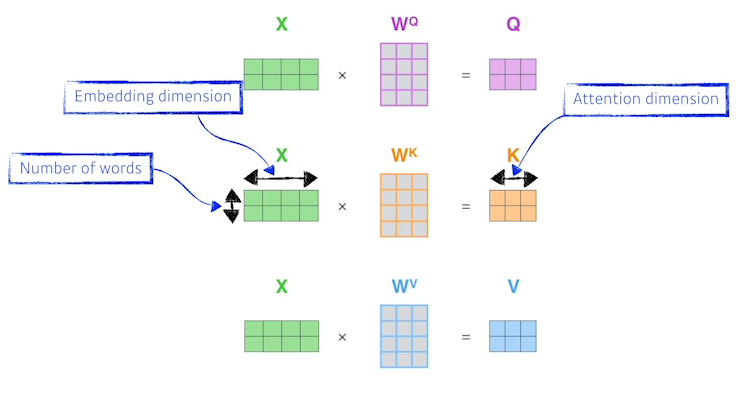
- Q, K, V를 구하는건 하나의 MLP가 있다고 생각하면 되고 모든 단어가 공유한다. X의 차원이 2, 4인것은 2개의 단어가 있고 단어를 embedding했을 때 4의 정보로 표현된다는 의미이다.
- 왜 잘될까??
- 이미지하나가 주어졌을 때 CNN MLP로 생각하면 입력에 따라 출력이 고정된다.
- Transformer은 네트워크가 고정되어 있어도 같이 들어오는 다른 입력이 달라짐에 따라 출력이 변화되고 이러한 특성으로 더 많은것을 표현할 수 있다.
- 한계
- RNN은 매우 큰 입력이 들어오면 각 단어별로 나누어 단순히 여러번 돌리면 오래걸리지만 동작한다.
- 하지만 Transformer는 N개의 단어를 한번에 처리해야하고, 한번에 처리해야하는 입력양이 $N^2$이기 때문에 큰 입력에대해서 처리하기 힘들다.
Multi-headed attention(MHA)
- 앞에서 Attention을 여러번 하는것
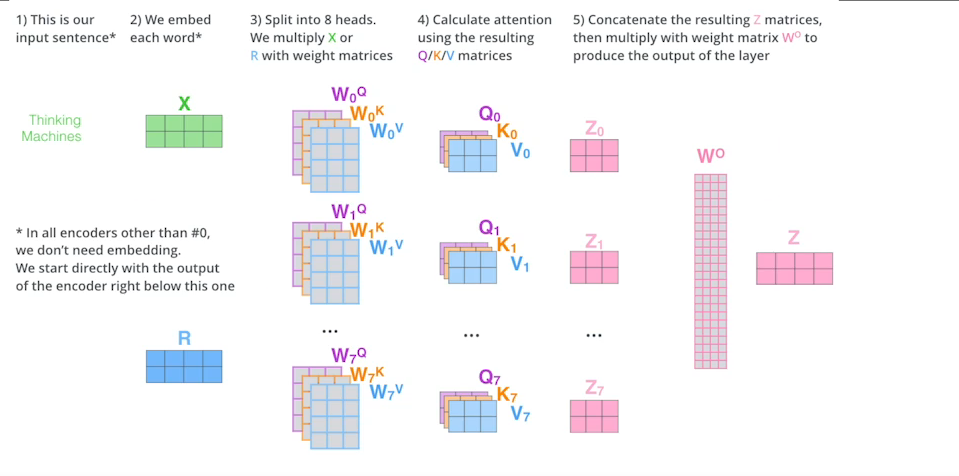
- 하나의 embedding된 벡터에 대해서 Q, K , V를 하나만 만드는것이 아니라 여러개를 만드는것이다.
- 이렇게 여러개의 벡터를 만들게 되면 N개의 인코딩된 벡터가 나오고 나온 인코딩된 벡터를 다음 인코더로 넘겨줘야한다. 그러기 위해서는 입력 차원과 출력 차원을 맞춰야한다. (Embedding된 벡터와, 인코딩되어서 Self attention으로 나온 벡터가 같은 차원이어야 한다.)
- 아래 그림에서는 나누어진 벡터들을 W를 곱해 차원을 맞춰준다. 하지만 실제 구현은 ..TODO
positional encoding
- 함께 들어오는 다른 입력을 고려하였지만 순서를 고려하지 않아 positional encoding과정이 필요하다.
- positional encoding은 특정 방법으로 벡터를 만든다. (특정 값을 더하는것)
디코더
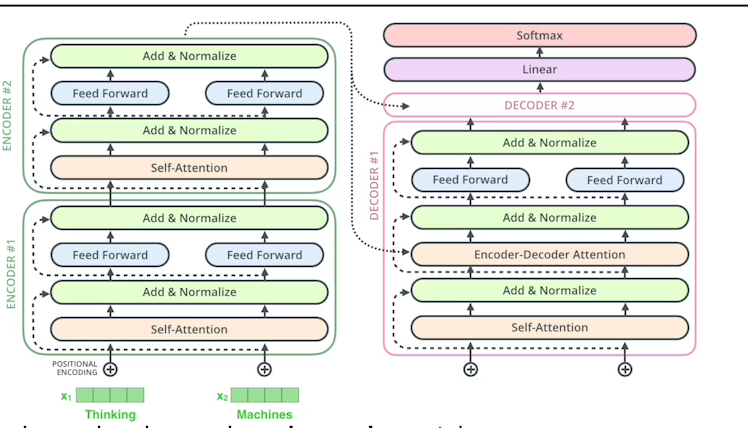
- 디코더로 Key와 value를 보낸다.
- i번째 단어를 만들 때 i번째의 Q벡터와 나머지 단어의 Key 벡터를 곱해서 attention을 만들고, value벡터를 weighted sum을 한다.
- input에 있는 단어들을 디코더에 있는 출력하고자 하는 단어들에 대해서 attention을 만들기 위해서는 input에 해당하는 벡터들의 key 벡터와 value벡터가 필요하다.
- 디코더에서 만들어지는 Query벡터와 입력으로 부터 얻어진 Key, Value벡터를 가지고 최종값을 출력한다.
- 최종은 Softmax를 거쳐 단어의 분포를 보고 매번 sampling하는 식으로 출력 단어가 나오게된다.
Vision Transformer
- Vision에서도 Transformer구조를 사용한다.
DALL-E
- 문장을 주면 알아서 이미지를 생성해준다.
- https://openai.com/blog/dall-e/