Home Generative 모델
Post
Cancel

Generative 모델

minsokim on Feb 5, 20212021-02-05T19:31:12+09:00

Generative 모델

  • Generative모델은 데이터를 학습해 데이터의 분포를 따르는 유사한 데이터를 생성하는 모델이다.
  • Generative 모델은 결합 확률 분포를 학습해 실제 클래스들의 분포를 모델링한다. 이러한 결합확률 분포 p(x,y)를 알게되면 가 주어졌을 때 가장 잘 맞는 x를 생성할 수 있다.
  • 엄밀한 의미의 Generative모델은 특정 이미지가 원하는 이미지가 맞는지 분류하는 모델이 내부에 포함되어 있다.(Density estimation, anomaly detection) 이러한 모델을 explicit 모델이 라고 한다.

Basic discrete Distributions

  • Bernoulli distribution (이항 분포)
    • D = {Heads, Tails}
    • P(X=Heads)=p 라면 P(X=tails) = 1 - p이다.
    • 파라미터가 하나만 있으면 확률을 나타낼 수 있다.
  • Categorical distribution
    • D = {1,…,m}
    • m - 1개의 파라미터 있으면 확률 표현 가능
  • Example
    • 각각의 pixel이 binary 인 image가 있을 때 하나의 이미지의 pixel수가 N이라면 가능한 상태의 개수는 $2^n$이다. $p(x_1,…,x_n)$을 나타내기 위한 파라미터 개수는 $2^n-1$이 된다.
    • 각 픽셀들이 서로 독립적이라고 하면 $p(x_1,…,x_n)=p(x_1)p(x_2)…p(x_n)$이 된다. 이 경우 가능한 상태의 개수는 $2^n$으로 똑같지만 이 distribution을 표현하기 위한 parameter는 n개만 있으면 된다.
  • 왜 fully dependent 필요한 파라미터가 $2^n-1$인가???
    • chain rule을 적용하면 쉽게 알 수 있다.
    \[p(x_1,...,x_n)=p(x_1)p(x_2|x_1)p(x_3)(x_1,x_2)...p(x_n|x_1,...,x_{n-1})\]

    • \(p(x_1)\) 은 한개의 파라미터만 있으면된다.

    • \(p(x_2|x_1)\) 은 \(p(x_2|x_1=0), p(x_2|x_1=1)\) 를 위한 파라미터 2개가 필요하다.

    • 위와 마찬가지 이유로 \(p(x_3|x_1,x_2)\) 는 4개의 파라미터가 필요하다.

    • 따라서 총 파라미터 개수는 $1 + 2+2^2+…+2^{n-1}=2^n-1$이 된다.

Conditional independence

  • 위의 예에서 볼 수 있듯이 fully dependent은 너무 많은 파라미터가 필요하고, fully independent는 이전 데이터를 전혀 고려하지 않는 문제가 있다.
  • Conditional independence는 fully dependent 와 fully independent사이의 적절한 합의점을 찾는 방법이라고 생각하면된다.
  • Conditional independence는 특별한 가정인데 $x\perp y|z$ 라고 가정하면 $p(x|y,z)=p(x|z)$임을 이용해 특정 개수에만 dependent하게하여 파라미터수는 fully dependent보다 줄이고, fully independent보다는 다른 데이터를 고려하게 할 수 있다.
  • markov assumption
    • 바로 직전의 데이터에만 dependent하다고 가정
    \[ㄱX_{i+1}\perp X_1,...,X_{i-1}|X_i\] \[p(x_1,...,x_n)=p(x_1)p(x_2|x_1)...p(x_n|x_{n-1})\]
    • 파라미터의 개수는 2n -1 개가 필요함을 알 수 있다.
  • Auto-regressive model은 이러한 conditional independence를 사용한 모델이다.

Auto-regressive Model

  • Auto-regressive Model 어떤 하나의 정보가 이전 정보에 dependent한 모델을 말한다.
  • 보통 이전 n개의 데이터를 고려하는걸 AR(n)모델이라고 한다.
  • 임의의 도메인에 Auto-regressive Model을 활용하려면 ordering이 필요하다.
    • ordering을 어떻게 하느냐에 따라 성능이 달라질 수 있다.
    • 어떤 conditional independence assumption을 주느냐에 따라 성능이 달라질 수 있다.

NADE(Neural Autoregressive Density Estimator)

gen1

\[p(x_i|x_{1:i-1})=\sigma(\alpha_ih_i+b_i)\\h_i=\sigma(W_{_{<i}x_{1:i-1}}+c)\]
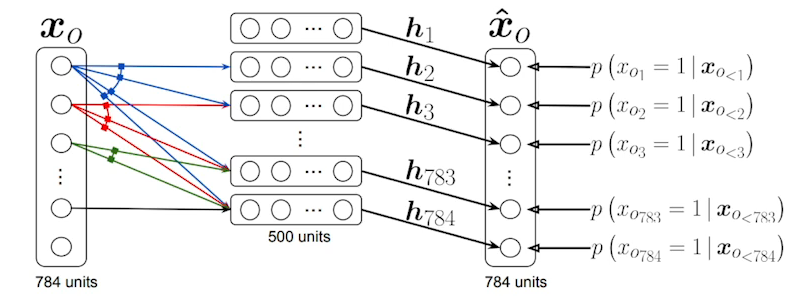
  • i번째의 픽셀일 첫번째 부터 i-1번의 픽셀과 dependent하게 하는 모델
  • 네트워크의 입장에서는 입력 차원이 계속달라져 W가 계속 커지게된다.
  • NADE는 explicit모델이다.
    • Generate만 할 수 있는 게 아니라 입력에 대한 확률을 계산할 수 있다.
  • 만약 연속랜덤 변수를 모델링할 경우 마지막 출력에 mixture of Gaussian을 사용하여 연속 분포를 만들 수 있다.

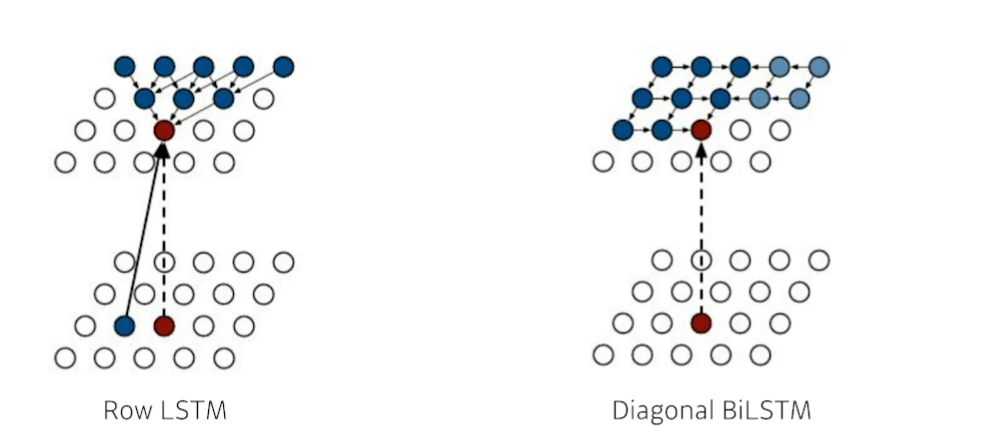
Pixel RNN

  • 이미지에 있는 픽셀을 generate하는 모델
  • n x n RGB image가 있을 경우 i번째 픽셀에 R을먼저만들고 G,B를 순서적으로 만든다.
  • NADE같은경우 Fully connected layer를 통해 만들었다.

  • Pixel RNN은 RNN을 통해 generate한다.

  • Ordering 에 따라 두가지 모델로 나뉜다.
    • Row LSTM
    • Digonal BiLSTM

gen2

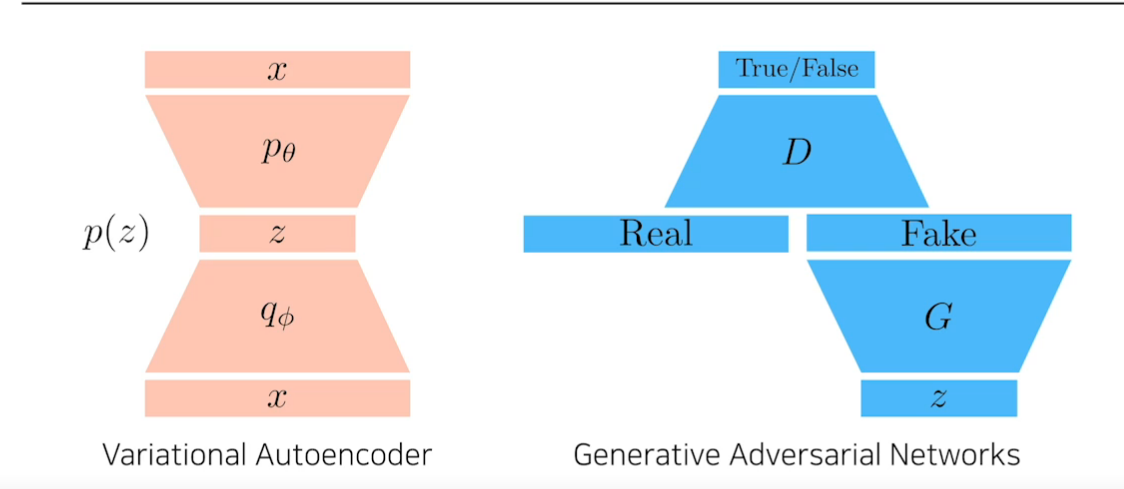
Variational Auto-encoder(VAE)

  • variational inference and deep learning :A new synthesis를 꼭 읽어보자
  • 일반적으로 아는 autoencoder는 Generative model이 아니다.
  • Variational inference(변론추론)
    • Variational inference의 목적은 Posterior distribution을 찾는것이다.
    • 내가 찾고자하는 Posterior distribution을 근사할 수 있는 Variational distribution을 찾는 과정을 VI라고한다.

    • Posterior distribution $p_{\theta}(z|x)$

      observation이 주어졌을 때 내가 관심있어하는 랜던변수의 확률분포

    • Variational distribution $p_{\phi}(z|x)$

      일반적으로 Posterior distribution를 계산하기 힘들기 때문에 Variational distribution로 근사하여 이를 최적화하는것으로 목적을 달성한다.

    • KL divergence를 사용해 Variational distribution와 Posterior distribution의 차이를 줄인다.
    • 하지만 실제 Posterior distribution을 모르는데 Variational distribution와 거리를 줄일 수 없다. 이걸 해결하는 방법이 ELBO이다.

    gen3

    • 실제 Posterior, Variational 의 거리를 줄이는게 목적이지만 불가능하기 때문에 ELBO를 계산하여 ELBO를 maximize하므로써 목적을 달성한다.
    • ELBO는 아래의 두개의 Term으로 나눌 수 있다.

    gen4

  • 논문 리뷰
  • 큰 문제점은 KL divergence를 사용하는 것인데 KL divergence는 내부에 적분이 들어있고 이를 미분하기 위해서는 closed form을 뽑아내야한다. 그래서 isotropic Gaussian을 활용한다.(Gaussian이 몇안되는 Closed form을 뽑아내는 분포이기 때문)

Adversarial Auto-Encoder

  • VAE의 Prior Fitting Term을 GAN으로 바꾼것이다.
  • VAE처럼 Gaussian만 뿐만 아니라 다양한 분포를 사용할 수 있다.
  • GAN을 사용해 latent distributions사이의 분포를 맞춰준다.

GAN

gen5

  • 참고 : 1시간만에 GAN 완전정복하기

  • Generator를 학습시키기 전에 실제 이미지로 Discriminator를 먼저 학습시킨다.

    → 진짜 이미지가 들어왔을때는 진짜이미지, Fake image가 들어왔을 때는 가짜라고 출력하는 모델을 학습시킨다.

  • Generator는 랜덤한 Code를 받아 이미지를 생성하고 생성한 이미지를 Discriminator가 진짜 이미지라고 판단하도록 학습을 진행한다.
\[\min_G\max_DV(D,G) = E_{x{\sim}p_{data}(x)}[logD(x)] + E_{z{\sim}p_{z}(z)}[log(1-D(G(z)))]\]
  • 위의 식은 GAN의 목적함수이다.식을 보면 Discriminator는 V(D,G)를 최대화 하도록, Generator는 V(D,G)를 최소화 하도록 학습한다.
  • Discriminator관점에서 목적함수를 최대화 시키기 위해서는 D(x)는 1, D(G(z))는 0이되야한다. D(x)가 1이되는것은 실제 데이터에 대해서는 True(1)을, 생성한 이미지에 대해서는 False(0)이 출력되도록 학습한다고 생각하면된다.
  • Generator관점에서 보면 Generator와 dependent한 항인 $E_{z{\sim}p_{z}(z)}[log(1-D(G(z)))$를 최소화 시키는것으로 학습한다. D(G(z))가 1이되면 해당 항이 최소가 되므로 생성한 이미지로 D를 속여 진짜 이미치처럼 생성하도록 한다고 생각하면된다.
  • 처음 G로 들어가는 z는 랜덤한 벡터(Latent code)이다. 이러한 랜덤한 벡터를 G에게 input으로 주면 이미지를 생성하고 D는 진짜 이미지인지 아닌지 판독한다.

실제 구현에서..

  • Generator는 $E_{z{\sim}p_{z}(z)}[log(1-D(G(z)))]$를 최소화 하도록 학습한다고 말하였지만 실제 처음 Generator는 굉장히 이상한 이미지를 생성할것이다. 이에 Discriminator는 실제 이미지가 아니라고 확신하여 D(G(z))는 거의 0에 가까운 값을 가지게된다.
  • log(1-x)그래프에서 x가 0일때 기울기가 작기 때문에 $E_{z{\sim}p_{z}(z)}[log(1-D(G(z)))]$를 최소화하는것이 아닌 $E_{z{\sim}p_{z}(z)}[log(D(G(z)))]$를 최대화 하도록 학습한다.
  • 이는 Generator가 안좋은 상태일때를 빨리 벗어나기 위함이다.
  • 코드상으로는 BCELoss에 fake label을 1로 주면된다.
1
2
3
4
5
6
7
8
9

criterion = nn.BCELoss()

# train D
loss = criterion(D(x), 1) + criterion(D(G(z)), 0)
....# backpropagation

# train G
loss = criterion(D(G(z)), 1)
...# backpropagation
  • 위와같은식으로 G를 업데이트하기위한 loss function을 생성하면 아래와 같은 loss가 나오므로 이를 최소화하는것으로 학습된다.
\[\min_G E_{z{\sim}p_{z}(z)}[-ylogD(G(z)) - (1-y)log(1-D(G(z)))]\]
  • 이때 label을 1로 넣어줬으므로 $E_{z{\sim}p_{z}(z)}[-ylogD(G(z))]$이 항을 최소화 하는 식이되고 이러한 negative log likelihood를 최소화하는것은 위에서말한 log likelihood 최대화 하는것과 같은 식이 된다.

왜 잘되는가??

\[\min_G\max_DV(D,G)\]
  • GAN의 목적함수인 위의 수식은 아래의 수식과 같다.
\[\min_{G,D}JSD(p_{data}||p_g)\\JSD(P||Q) = \frac{1}{2}KL(P||M) \frac{1}{2}KL(Q||M)~~~~~~where ~M = \frac{1}{2}(P+Q)\]
  • 따라서 GAN의 목적함수는 두 확률분포의 차이를 줄이는것이기 때문에 Generator가 실제 이미지에 가까운 이미지를 생성할 수 있게된다.

DCGAN

  • 기존 Discriminator에서는 Fully connected Layer를 사용했지만 DCGAN에서는 Convolution Layer를 사용한다.
  • Generator에서는 deconvolution을 사용한다.
  • pooling layer를 사용하지 않았다.
  • Adam optim을 사용
  • z벡터의 산술연산을 통해 특정 이미지를 생성할 수 있다.(예를들면 금발남자를 나타내는 z벡터에서 금발아닌 남자를 나타내는 z벡터를 뺀뒤 여자를 나타내는 z벡터를 더해주면 금발인 여자가 나오는…..)

info-GAN

  • 학습을 할 때 z만을 가지고 이미지를 만드는것이 아닌 C라는 Condition을 주어 특정 이미지를 생성할 수 있도록

Text2Image

  • 텍스트를 주면 이미지 생성

Puzzle-GAN

  • 원래의 이미지를 복원

CycleGAN

  • 이미지의 도메인을 변경하는 GAN
  • 예를들면 말이미지를 주었을 때 얼룩말로 바꾸는등…
  • 얼룩말을 그냥 말 사진으로 변경하는 모델
    • Discriminator에게는 일반 말 사진만 주어 학습한다.
    • Generator에게 얼룩말 이미지를 주어 생성하면 Discriminator는 일반 말이 나올때까지 False가 나오고 Generator는 Discriminator를 속이기 위해 학습해 일반 말 사진을 생성하게된다.
    • 원하는것은 같은 이미지에서 말의 색상만 바뀌는것이다 하지만 Generator가 원본이미지와 아예 다른 일반 말 이미지를 생성한다면 Discriminator는 이를 True로 볼것이다.
    • 원하는 결과를 얻기위해 이러한것을 막아주어야한다. (모양을 유지해야한다.)
    • 모양 유지를 위해 아래의 그림처럼 얼룩말을 말로 바꾸고 다시 얼룩말로 바꾸도록한다.

    gen6

DL
Python Pytorch Generative Model GAN VAE NADE
This post is licensed under CC BY 4.0 by the author.
Recent Update
Contents

RNN

Transformer