CNN(Convolutional Neural Networks)

기존 이미지를 학습할 때는 이미지의 형상을 고려하지 않고 raw data를 직접 처리하여 많은 학습 데이터가 필요하고, 학습시간이 많이 필요하였다. CNN은 이미지 공간정보를 유지한채 학습을 하는 모델이다.
Convolution Layer와 Pooling Layer를 여러 겹 쌓는 형태로 구성된다.
인반적인 CNN은 마지막 단에는 분류를 위한 Fully connected Layer가 추가된다.
최근에는 뒷단에 있는 Fully connected Layer를 줄이는 추세이다. 이러한 이유는 모델의 parameter가 늘어날 수록 generalization performance가 떨어지기 때문에 parameter를 줄이기 위해 Fully connected Layer줄인다.

Convolution

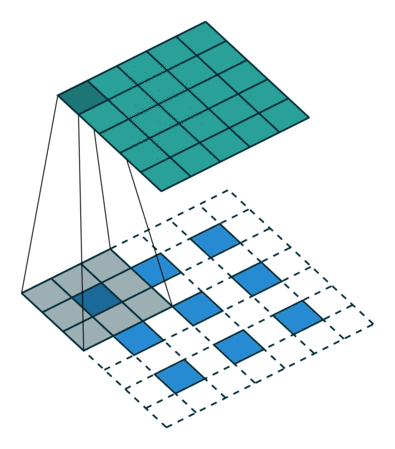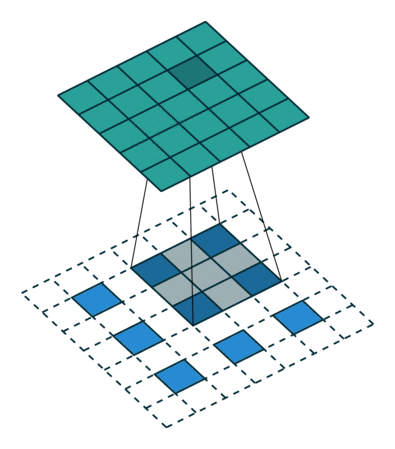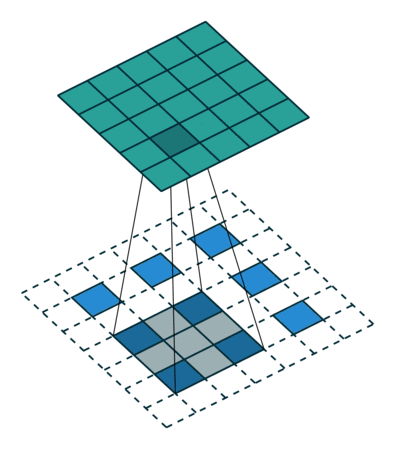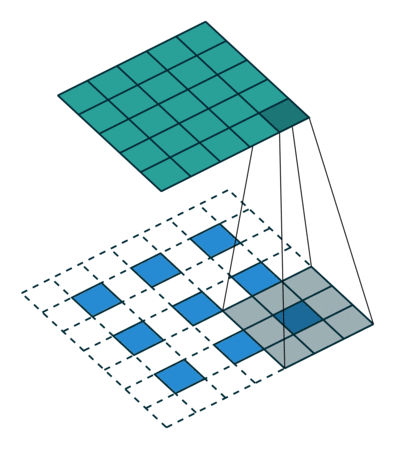
Convolution 연산은 기존 MLP(Fully connected)의 연산과 다르게 커널(filter)을 입력벡터 상에서 움직여가면서 선형 모델과 합성함수가 적용되는 구조이다.

\[h_i=\sigma(\sum_{j=1}^kV_jx_{i+j-1})\]

커널(filter)이 고정된 크기이기 때문에 파라미터 크기를 줄일 수 있다.
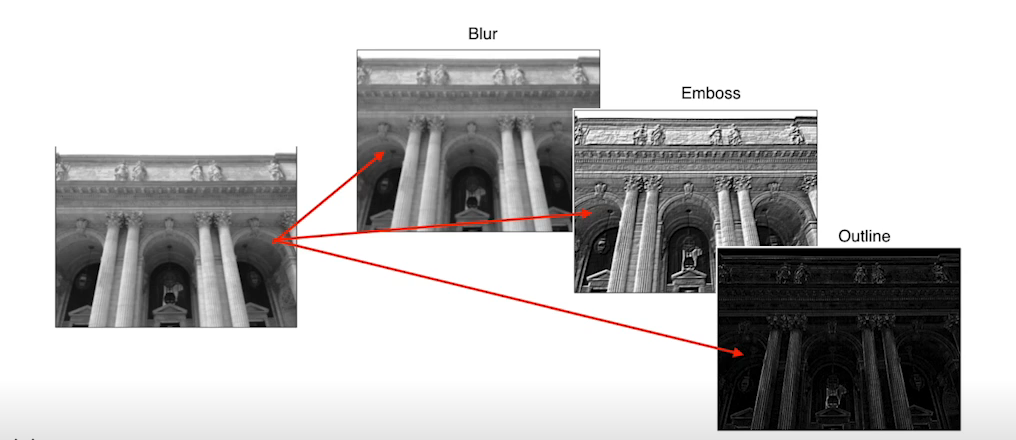
2D Convolution을 한다는말은 필터를 이미지에 찍는다고 생가하면 된다. 위의 사진처럼 필터에 따라 출력이 다양하게 나올 수 있다. 예를들어 3 * 3의 filter를 사용하고 각각의 값에 1/9 이들어가 있다면 평균이 출력될 것이므로 블러처리된 출력을 얻을 수 있다.

convolution 연산 이해

Convolution 연산의 수학적 의미는 신호(g)를 커널(f)을 이용해 국소적으로 증폭 또는 감소 시켜 정보를 추출 또는 필터링하는 것이다.
continuous
\[[f*g]=\int_{ℝ^d}f(z)g(x-z)dz=\int_{ℝ^d}f(x - z)g(z)dz=[g*f](x)\]
discrete
\[[f*g](i)=\sum_{a\in ℤ^d}f(a)g(i-a)= \sum_{a\in ℤ^d}f(i-a)g(a)=[g*f](i)\]
커널(filter)은 정의역 내에서 움직여도 변하지 않고(Translation invariant) 주어진 신호에 국소적으로 적용한다.
간단하게 말하면 2D Convolution을 한다는말은 필터를 이미지에 찍어 값을 누적한다고 생각하면 된다. 아래 사진처럼 필터에 따라 출력이 다양하게 나올 수 있다. 예를들어 3 * 3의 filter를 사용하고 각각의 값에 1/9 이 들어가 있다면 평균이 출력될 것이므로 블러처리된 출력을 얻을 수 있다

CNN1

다양한 차원에서의 Convolution

1D-conv
\[[f*g](i)=\sum_{p=1}^d f(p)g(i+p)\]
2D-conv
\[[f*g](i,j)=\sum_{p,q} f(p,q)g(i+p, j+q)\]
3D-conv
\[[f*g](i,j,k)=\sum_{p,q,r} f(p,q,r)g(i+p,j+q,k+r)\]
커널(filter)이 위치에 따라 변화되지 않는다.

Convolution 출력

출력의 높이 OH = (H + 2P - FH)/S + 1
출력의 폭 OW = (W + 2P - FW)/S + 1
P : 패딩 사이즈
S : Stride 사이즈
FH, FW : 필터의 높이, 폭
H, W : 입력의 높이, 폭

stride

input에서 커널(filter)이 움직이는 칸수를 말한다. 2D이상의 Convolution에서는 각 dim에 적용할 stride를 지정할 수 있다.

padding

convolution layer에서 Filter와 stride의 작용으로 Feature Map의 크기는 입력데이터보다 작아지게 된다. 이를 방지하기 위해 padding 기법을 사용한다. 입력데이터의 외각에 지정된 픽셀만큼 특정 값을 채워넣는것을 말한다.

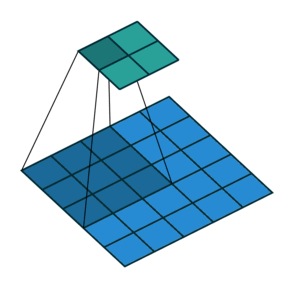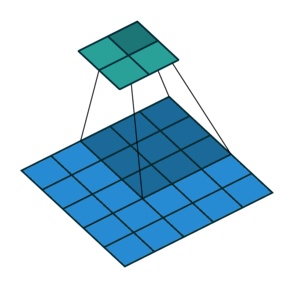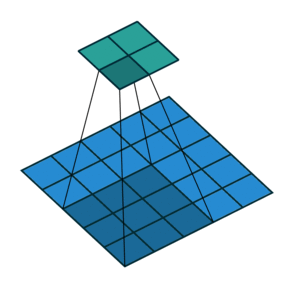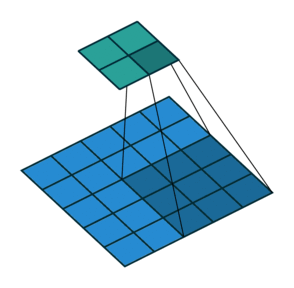
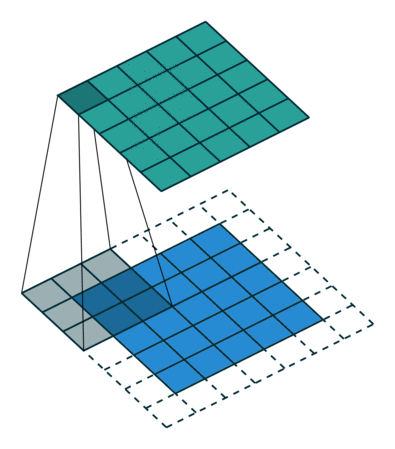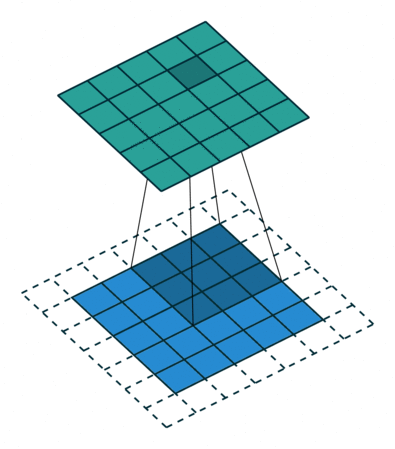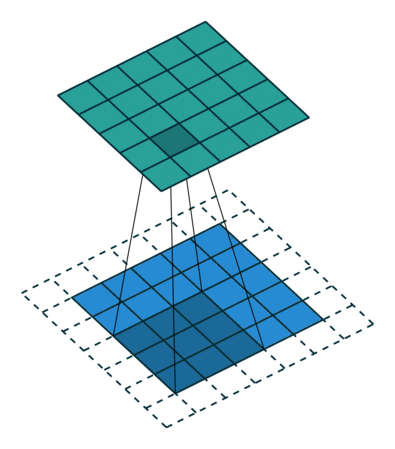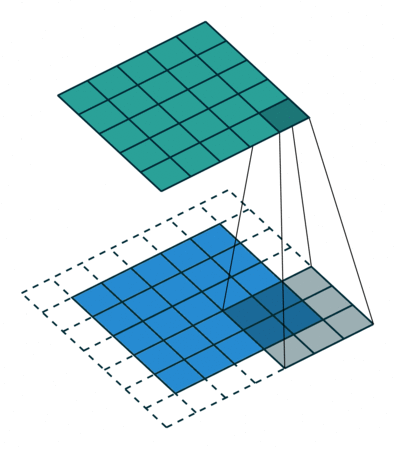
3 x 3 filter를 썻을 때 padding이 없는 경우와 padding size가 1인 경우를 비교한 모습이다.

이처럼 원하는 출력을 padding과 stride를 주는것으로 만들 수 있다.

pooling 레이어

Convolution Layer의 출력 데이터를 입력으로 받아서 출력의 크기를 줄이거나 특정 데이터를 강조하는 용도로 사용된다.

Max Pooling
- 입력데이터에서 Pooling size만큼 씩 나누어 최대값만 사용한다.
Average Pooling
- 입력데이터에서 Pooling size만큼 씩 나누어 평균값을 사용한다.
Min Pooling
- 입력데이터에서 Pooling size만큼 씩 나누어 최소값만 사용한다.

보통 Pooling크기와 Stride를 같은 크기로 처리해 각 원소가 한번씩만 처리되도록 한다.

채널

컬러 사진 데이터의 shape는 (H, W, 3)으로 표현된다(R, G, B). 흑백의 경우 (H, W, 1)로 표현되는데 가장 마지막에 있는 것이 채널이다.
채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 된다.
사용한 필터의 개수만큼 출력이 나오기 때문에 여러개의 필터를 사용하면 출력의 채널은 필터의 개수와 같게 나온다.

CNN2

CNN3

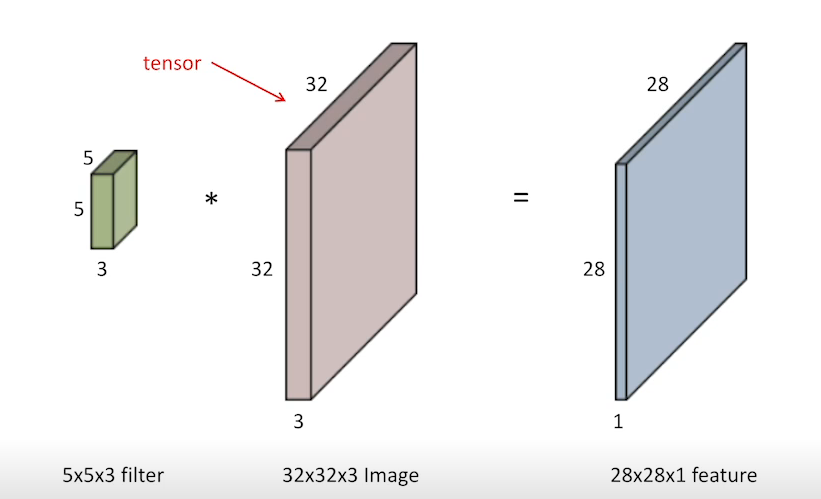
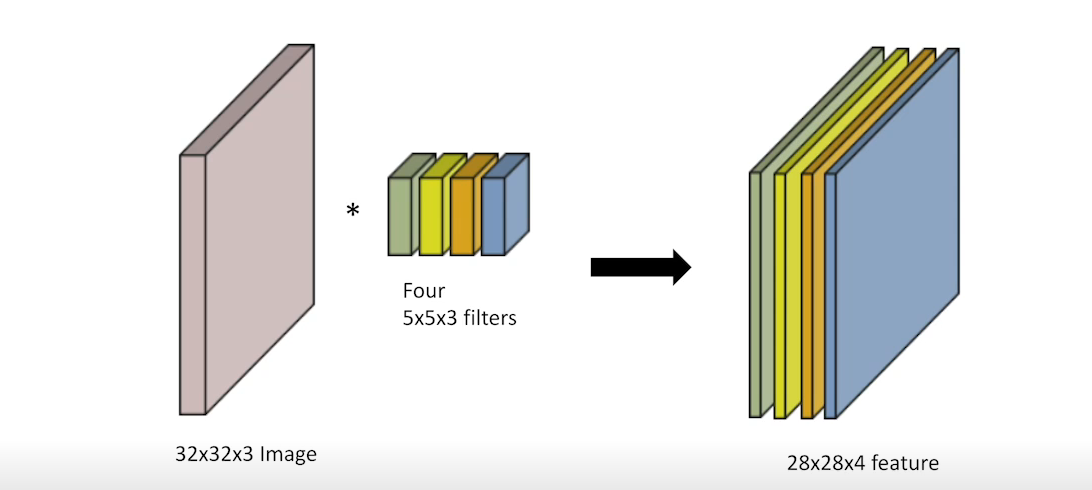
convolution 연산의 역전파

Convolution연산은 필터가 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 Convolution 연산이 나온다.

\[\frac{\partial}{\partial x}[f*g](x)=\frac{\partial}{\partial x}\int_{ℝ^d}f(y)g(x-y)dy\\=\int_{ℝ^d}f(y)\frac{\partial g}{\partial x}(x-y)dy\\=[f*g'](x)\]

Parameter

특정 모델을 보고 각 Layer별로, 그리고 전체 모델에서 파라미터가 몇개정도 필요한지 아는것이 중요하다.

CNN4

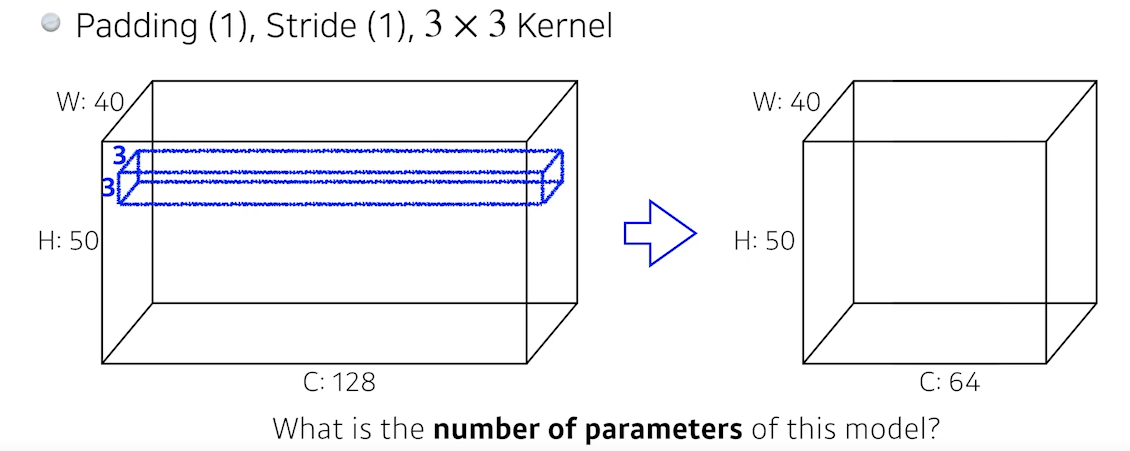
3 x 3 x 128의 필터를 사용하면 1겹의 feature map이 나오므로 64채널을 가진 feature map을 가지려면 이러한 필터가 64개 있어야 한다. 따라서 parameter 수는 3 x 3 x 128 x 64개 이다.

CNN5

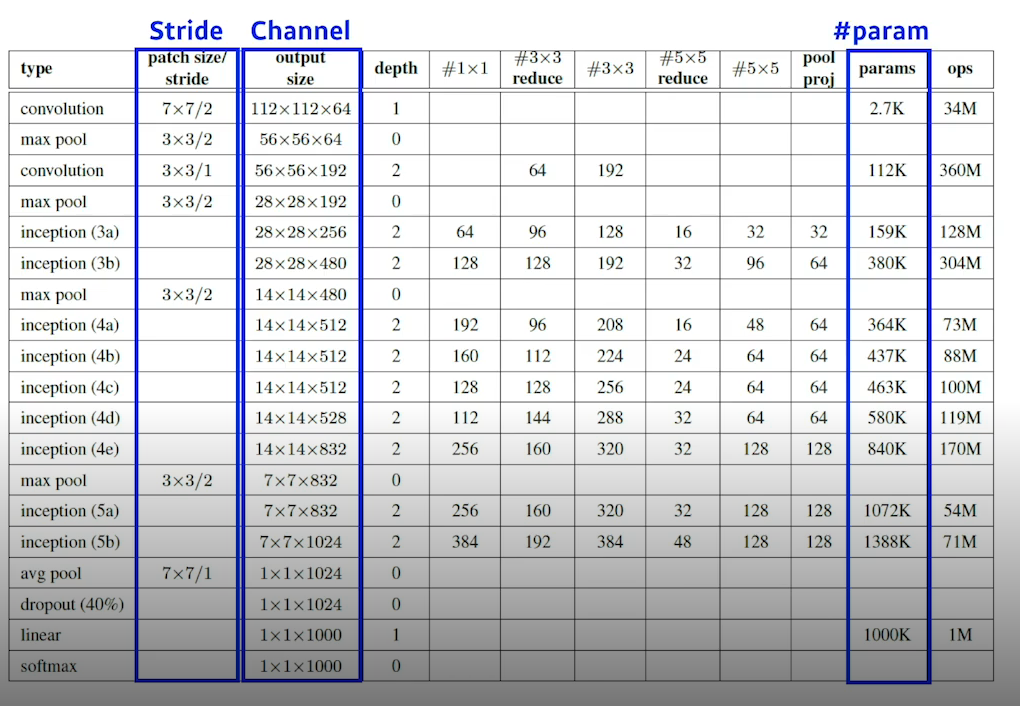
특정 모델을 보았을 때 파라미터가 몇개가 되는지 아는것은 중요하다. 직접손으로 한번 계산해보자

Dense Layer와 Parameter 개수

CNN6

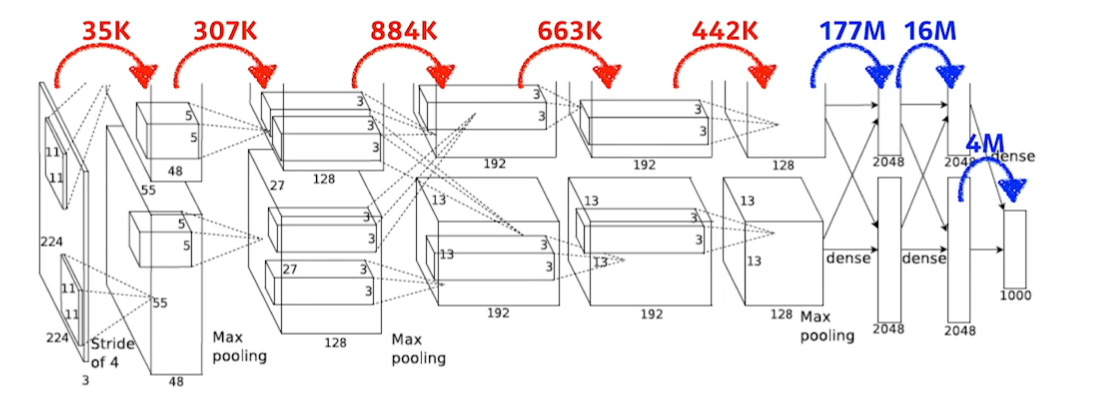
AlexNet의 각 Layer별 파라미터 수를 계산하면 위의 그림과 같다. parameter숫자가 dense layer로 넘어가면서 급격하게 늘어나는것을 볼 수 있다. 이러한 이유는 convolution은 하나의 필터가 모든 위치에 적용되지만 Fully connected Layer는 input의 개수 * output의 개수만큼의 Parameter가 필요하기 때문이다.
뉴럴네트워크의 성능을 올리기 위해서 Parameter를 줄이는게 중요한데 대부분 Parameter가 들어가 있기 때문에 뒷단의 Fully Connected Layer를 최대한 줄이고 앞단의 convolution layer를 최대한 깊게 쌓으려고 하는것이 트랜드이다.

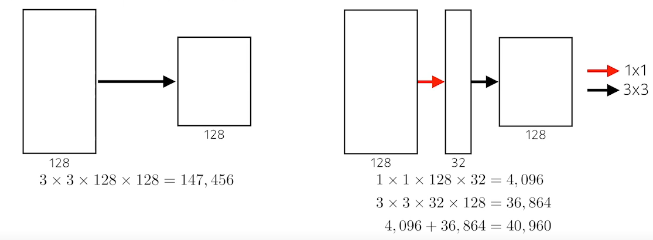
1 x 1 Convolution

채널을 줄이는 역할을 한다. 이는 곧 파라미터 수를 줄일 수 있음을 의미한다.
CNN의 깊이는 늘리면서 파리미터는 줄일 수 있다.
대표 : bottleneck architecture

CNN 모델들

AlexNet

CNN8

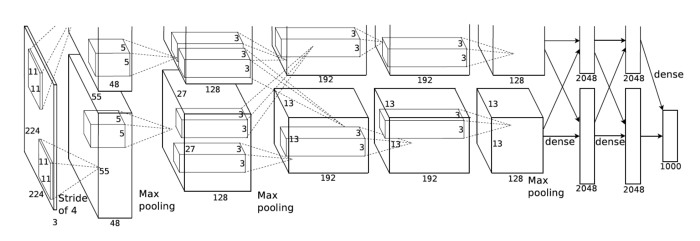
5개의 Convolution Layers와 3개의 Dense Layers를 가지는 모델이다.
첫 입력의 11 x 11의 필터를 사용하는데 최근은 7 x 7을 거의 벗어나지 않는다. VGGNET에서 3 x 3을 쓴 이유와 같은 이유이다.
ReLU를 사용하였다.
GPU활용
Local response normalization, Overlapping polling
- LRN : 어떤 입력 공간에서 response가 많이 나오는것을 죽이는것
data augmentation
Dropout

VGGNet

CNN9

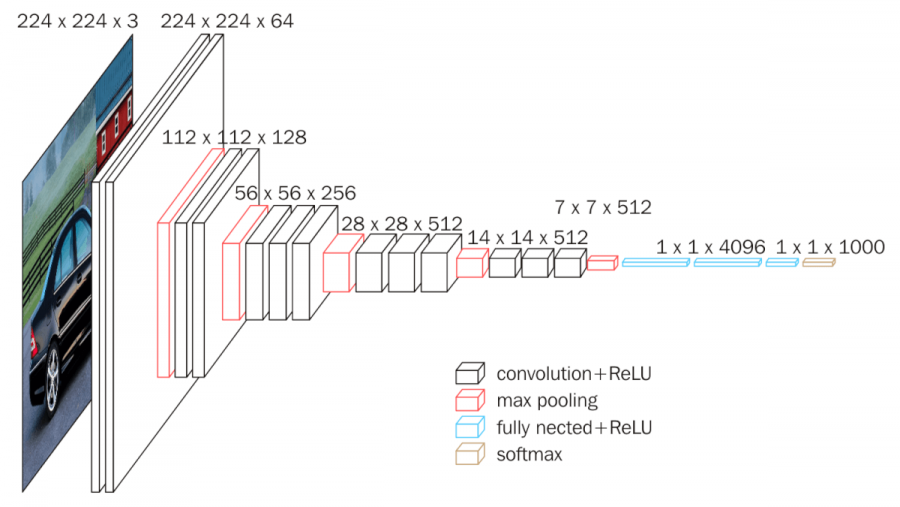
3 x 3 filter만 사용하였다.
- filter가 커질수록 고려되는 input의 크기가 커진다. 이것을 receptive field라고 하는데 (filter size == receptive가 맞나?? TODO) 아래의 그림처럼 3 x 3을 두번 사용하면 5 x 5를 한번 사용하는 것보다 적은 parameter가 필요하지만 receptive filed는 같다.
- receptive: 출력 레이어의 뉴런 하나에 영향을 미치는 입력 뉴런들의 공간 크기

GoogLeNet

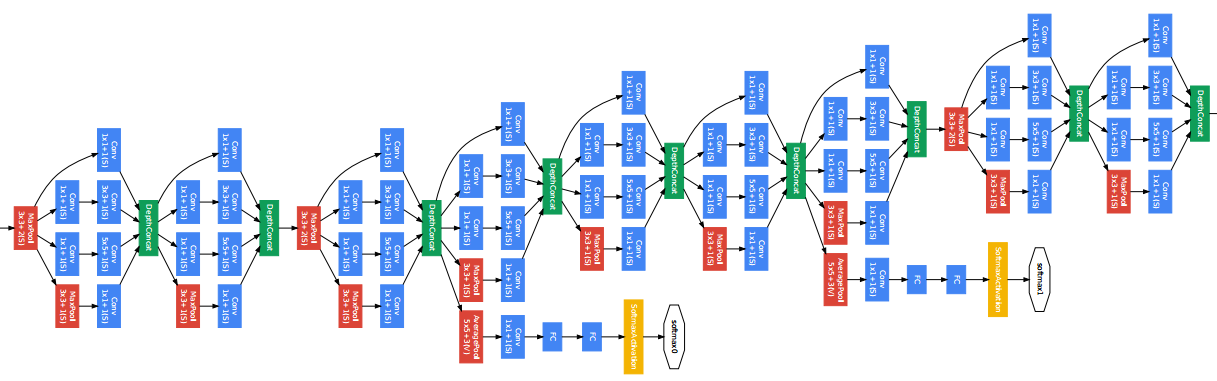
CNN11

여러 네트워크가 들어가 있는 이러한 구조를 NiN(Network in Network)구조라고 한다.
GoogLeNet은 22개의 Layer로 구성되어있고
GooglLeNet은 NiN구조와 Inception Block을 잘 이용하였다.

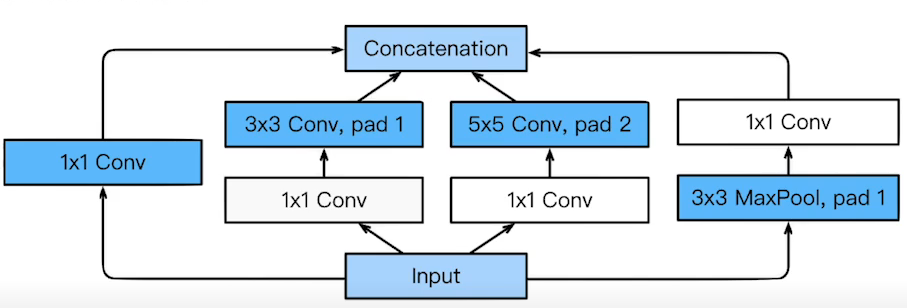
CNN12

inception Block은 여러개의 receptive field를 가지는 필터를 거쳐 어러개의 response를 Concatenation한다. 이러한 구조 중간에 1 x 1 Convolution을 추가해 Parameter를 줄였다.

ResNet

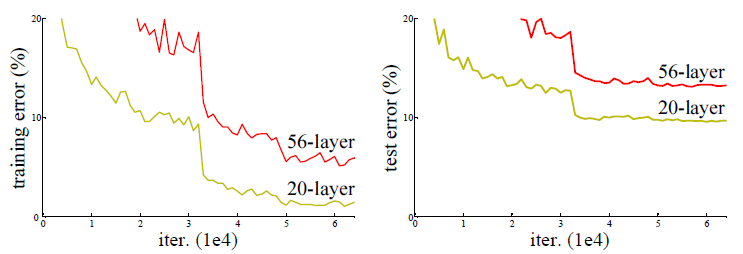
CNN13

ResNet논문에는 위와 같은 그래프가 있는데 이는 기존의 방식대로는 어느 정도 네트워크가 커지면 depth가 더 낮은 모델보다 학습이 되지 않는다는 것을 보여준다.
위의 문제점을 해결하기 위해 ResNet은 identity map(Skip connection)을 추가하였다.

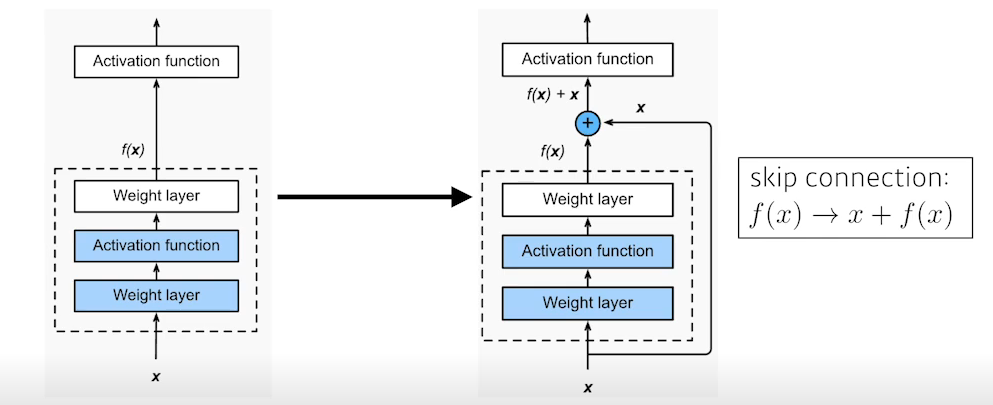
CNN14

이러한 ResNet은 network를 더 deep하게 쌓을 수 있는 가능성을 열어주었다.

Dense Net

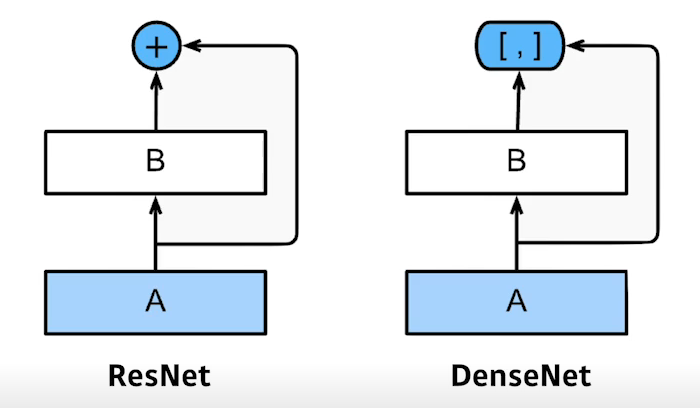
CNN15

Dense Net은 ResNet처럼 더하는 것이 아닌 concatenation하는 방법을 제시하였다.
concatenate하면 채널이 점점 커지는데 깊이가 깊어지면 계속해서 기하급수적으로 커지게된다.
이런 문제를 사용하기 위해 1 x 1 Conv를 사용해 채널을 줄인다.

semantic Segmentation

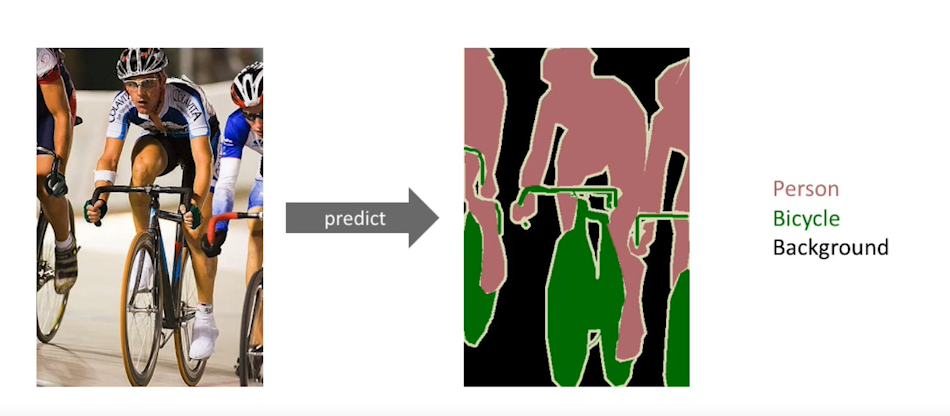
CNN16

이미지의 픽셀이 어떤 label에 해당하는지 찾는 문제, 자율주행등에 사용된다.

Fully Convolutional Network

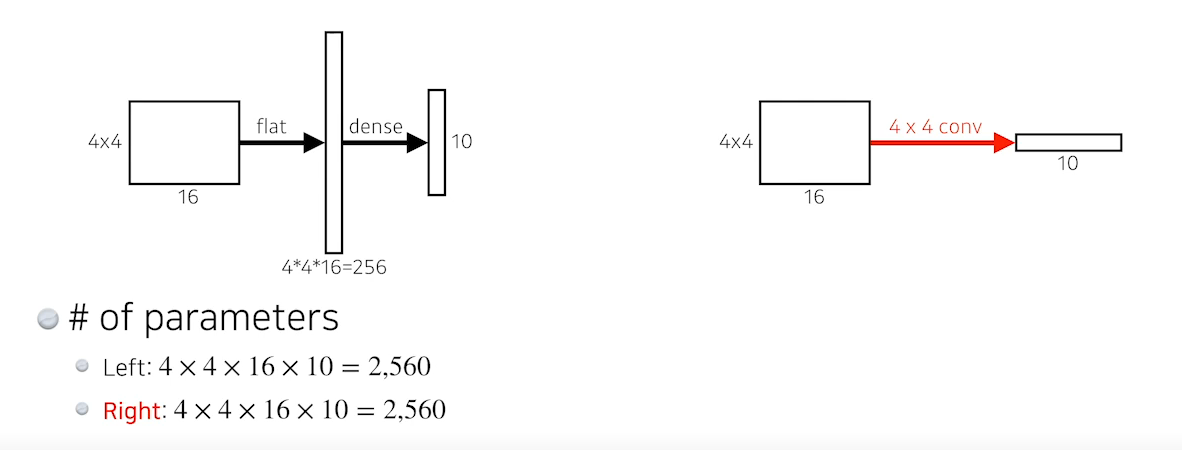
CNN17

Dense Layer를 없애 output Layer도 Conv Layer를 사용하는 네트워크를 말한다. 이렇게 Dense Layer를 없애는것을 convolutionalization이라고 한다.
parameter수가 줄지는 않는다(Fully connected가 하던것과 동일한 역할을 단순히 Conv 연산으로 바꾼것 뿐).
기존 Fully Connected 네트워크는 input의 size에 의존적이다. 하지만 Fully Convolutional 네트워크는 입력의 크기와 상관없이 동일한 Filter를 사용하기 때문에 작동한다.
하지만 입력의 크기가 줄어들면 Output의 크기도 줄어들기 때문에 원래의 size로 늘려주는 역할이 필요하다.
- Deconvolution(conv transpose)
  실제 Conv의 역연산은 아니지만 실제 모델을 설계할 때 Conv의 역 연산이라고 생각하면 편하다.

Detection

R-CNN

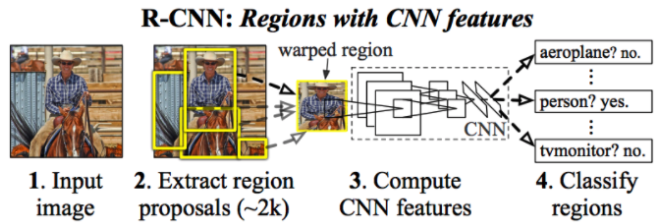
CNN18

전체적인 프로세스는 위의 사진과 같다.
1. Image입력
2. Selective Serarch 알고리즘으로 regional proposal output약 2000개 추출
3. CNN을 사용하기 위해 동일한 사이즈로 Warp
4. 약 2000개의 warped된 이미지를 CNN모델에 넣는다.
5. 각각의 결과에 대해 분류한다.
region proposals은 물체가 있을것 같은곳을 찾는다. (Selective search 알고리즘)
이러한 R-CNN은 CNN을 2000번이나 수행해야한다.

SPPNet

CNN19

R-CNN과 비슷하나 하나의 이미지에 대해서 한번만 CNN을 수행하면 되도록 한 네트워크이다.
Conv Layer와 FC layer사이에 있는 SSP는 입력에 상관없이 고정된 Feature map을 출력해 주기 때문에 R-CNN에서 Wrap하는 과정에서 발생되는 왜곡을 막을 수 있다.
TODO : 동작 방식이 이해되지 않는다..?

Fast R-CNN

기존 SPPNet, R-CNN과 다르게 end-to-end 모델을 제시하여 학습을 간소화시키고 정확도와 성능 모두를 향상시킨 네트워크

Faster R-CNN

bounding box를 뽑아내는 Region Proposal을 학습시키는것(RPN)
- Region Proposal Network
  - RPN은 이미지의 특정 영역이 bounding박스로서 의미가 있는지 없는지를 찾는다.
  - RPN을 학습시키기 위해 anchor boxes가 필요한데 이는 미리 정해둔 bounding box 크기를 말한다.
  - 3개의 region size와 3개의 ratios를 나타낼 9개의 파라미터, bounding box를 얼마나 키우고 줄일지 결정하기 위한 4개의 파라미터, box가 유의미 한지를 나타내는 2개의 파라미터로 총 9 * (4+2)의 파라미터가 필요하다.
논문 리뷰 자료

YOLO(v1)

Faster R-CNN에서는 Region Proposal 네트워크가 있었고 분류는 이 뒤의 네트워크가 처리하였는데 YOLO는 한번에 이런 작업을 진행한다.
이미지가 들어오면 S x S grid로 나눈다.

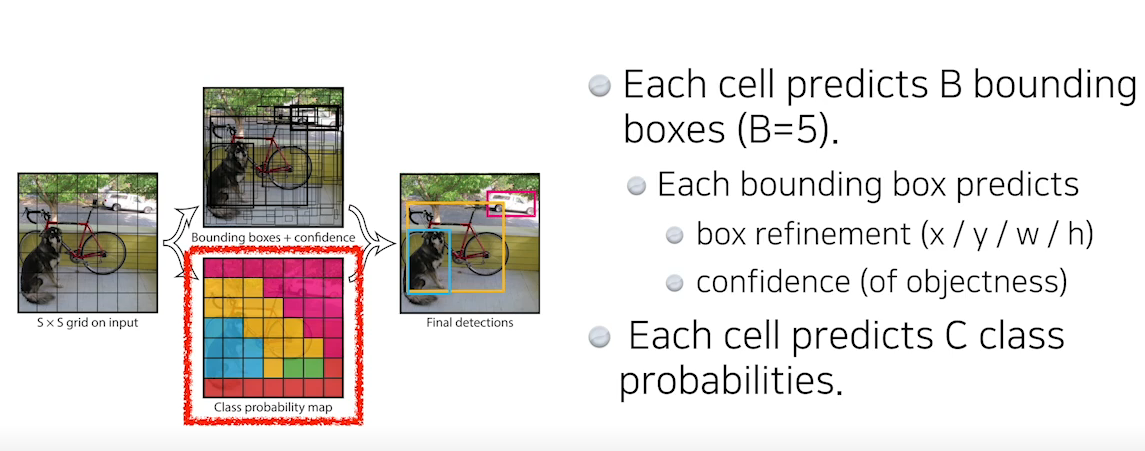
CNN20

grid Cell이 해당물체의 Bounding box와 해당 물체가 무엇인지를 같이 예측한다.
프로세스
1. 이미지를 S x S grid로 나눈다.
2. B개의 bounding box의 x, y, w, h와 유의미한 box인지를 찾고 동시에 해당 gird cell이 이 어느 Class에 속하는지 예측한다.
S x S의 Grid에서 5개(x,y,w,h, confidence)의 offset을 가지는 B개의 bounding box를 C개의 클래스로 구분하기 때문에 총 S x S x (B * 5 + C)의 Tensor된다.
YOLO(V1) 논문 리뷰

CNN