벡터
- 벡터란 숫자를 원소로 가지는 리스트 또는 배열이다.
벡터는 공간에서 한 점을 나타낸다(원점을으로부터 상대적 위치)
→1차원에서는 (x), 2차원에서는 (x,y), 3차원에서는 (x,y,z)…
- 벡터에 숫자를 곱하면 길이만 변한다. 숫자가 0보다 작을 경우 방향은 반대 방향이된다.
- +, -연산은 같은 크기의 벡터끼리만 연산이 가능하고 같은 위치의 원소를 +, -한것이다.
- 두 벡터의 덧셈, 뺄셈은 다른 벡터로부터의 상대적 위치 이동을 표현한다.
성분곱(hadamard product)
같은 위치의 원소끼리의 곱(numpy에서의 *)
벡터의 노름(norm)
norm 원점에서 부터의 거리를 말한다. norm의 경우 여러가지가 있는데 $l_{1}norm과 l_{2}norm$이 대표적이다. 다양한 노름이 존재하는 이유는 노름에 종류에 따라 가하학 성질이 달라지기 때문이다.
머신러닝에선 각 성질들이 필요할 때가 있으므로 필요에 따라 norm을 선택해서 사용해야한다.
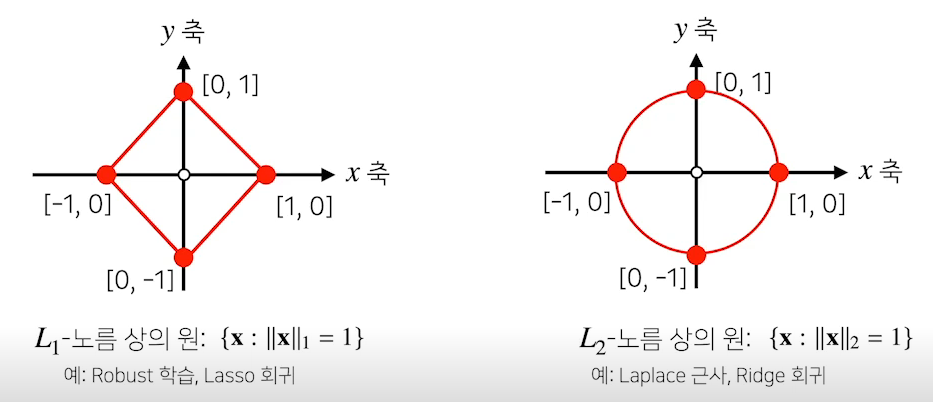
- L1-노름은 성분의 변화량의 절대값을 모두 더한다.
- 좌표 평면에서 좌표축을 따라 이동한 거리를 말한다.
1
2
3
4
def l1_norm(x):
x_norm = np.abs(x)
x_norm = np.sum(x_norm)
return x_norm
- L2-노름은 피타고라스 정리를 이용해 유클리드 거리를 계산한다.
1
2
3
4
5
def l2_norm(x):
x_norm = x*x
x_norm = np.sum(x_norm)
x_norm = np.sqrt(x_norm)
return x_norm
두 벡터 사이의 거리
두 벡터사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다. $L_{1}, L_{2} norm$ 을 이용해 두 벡터 사이의 길이를 계산할 수 있다.
두 벡터 사이의 각도
각도는 $L_{2}norm$ 에서만 계산할 수 있다. 제 2 코사인 법칙을 사용해 두 벡터 사이의 각도를 계산할 수 있다. $a = b^2 + c^2 - 2bccosA …$
두 벡터 x,y의 거리는 $||{x}-{y}||_{2}$ 이므로 두 벡터 사이의 각도 A는
\[cosA = \frac{|| {x} || ^ 2_ {2} + || {y} || ^ 2_ {2}-|| {x}-{y} || ^ 2_ {2} }{ 2 || {x} || _ {2} || {y} ||_{2}}\]로 구할 수 있다. 다른 차원에서의 각도도 L2 norm을 사용해 계산할 수 있다.
분자의 경우 식을 $X(x_{1},x_{2}), Y(y_{1},y_{2})$ 를 넣어 정리해보면
\[|| {x} || ^ 2_ {2} + || {y} || ^ 2_ {2}-|| {x}-{y} || ^ 2_ {2} = 2(x_{1}y_{1} + x_{2}y_{2})\]로 정리될 수 있다. 벡터의 내적은 각 벡터의 성분곱을 한뒤 더하는것이므로
분자는 2x내적이 된다. 따라서 위의식은 아래식으로 나타낼 수 있다.
\[cosA = \frac{<{x},{y}>}{||{x}||_{2}||{y}||_{2}}\]1
2
3
4
def angle(x,y):
v = np.inner(x,y)/(l2_norm(x) * l2_norm(y)) # np.inner는 내적을 구해준다.
theta = np.arccos(v)
return theta
내적
내적은 정사영(orthogonal projection)된 벡터의길이와 관련있다.
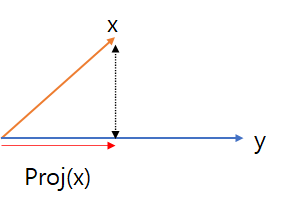
위의 그림에서 Proj(x)는 벡터 y로 정사용된 벡터 x의 그림자를 의미한다. 이때 Proj(x)의 길이는
코사인법칙에 의해 원래 벡터 X의 길이에 Cos(사이각)을 곱한 $||{x}||cosθ$ 가 된다.
내적은 정사영의 길이를 벡터 y의 길이 $||{y}||$ 만큼 조정한 값이다.
\[||{y}||Porj(x) = ||{x}||_{2}||{y}||_{2}cosθ\]내적은 두 벡터의 유사도를 측장하는데 사용가능하다.
행렬(matrix)
벡터를 원소로 가지는 2차원 배열이다. 행(row) 열(column)이라는 index를 가진다.
특정 행(열)을 고정하면 행(열)벡터라고 부른다.
행렬은 여러개의 벡터로 이루어진 배열이기 때문에 행렬은 여러 점들을 나타낸다고 생각하면 된다.
전치행렬
행과 열의 index가 바뀐 행렬을 말한다.
행렬 곱셈
행렬곱은 X의 열의 개수와 Y의 행의 개수가 같아야한다.
i번째 행벡터와 j번째 열벡터사이의 내적을 성분으로 가지는 행렬을 계산한다.
1 2 3
x = np.array([[1,2,3],[4,5,6],[7,8,9]]) y = np.array([[0,1],[1,-1],[-2,1]]) x @ y
행렬 내적
numpy의 inner함수를 사용해 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산할 수 있다.(수학에서 말하는 내적과 다름) X와 Y의 행의 크기가 같아야한다.
X라는 행렬과 Y행렬의 전치행렬의 행렬곱을 한것이 numpy의 inner이다.
행렬과 벡터
행렬은 벡터공간에서 사용되는 연산자로 이해한다. 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다. m차원의 벡터를 n*m행렬과 행렬곱하여 n차원으로 변경할 수 있다.
행렬곱을 통해 패턴을 추출할 수 있고, 데이터를 압축할 수 있다.
역행렬
역행렬은 행과 열의 숫자가 같고 행렬식이 0이 아닌경우에만 계산할 수 있다.
1 2
x = np.array([[1,2,3],[2,3,4],[4,5,6]]) np.linalg.inv(x) # 역행렬 계산
$XX^{-1} = X^{-1}X = I(항등행렬)$
- 유사역행렬(pseudo-inverse) 또는 무어펜로즈(Moore-Penrose)역행렬 $A^{+}$
축소 SVD(singular value Decomposition) 특이값 분해
A 가 m x n행렬이고, rank가 k일 때
$A = UΣV^T$로 분해가 가능하고 ,U는 m,k직교 행렬, Σ는 k,k행렬, $V^T$는 k,n직교 행렬
축소 SVD를 사용해 행과 열이 달라도 유사 역행렬을 구할 수 있다.
$A^{-1}=(UΣV^T)^{-1}=(V^T)^{-1}Σ^{-1}U^{-1} = VΣ^{-1}U^T$ 형태로 역행렬을 나타낼 수 있다. 이런 형태의 식을 유사 역행렬이라고 한다.(A가 가역 행렬이라면 위의 식이 역행렬이 되고, 아닐경우 유사 역행렬이 된다.)
행의 개수가 열의 개수보다 많을 경우$A^+=(A^TA)^{-1}A^T, A^+A = I$
→ left inverse matrix
열의 개수가 행의 개수보다 많을 경우 $A^+=A^T(AA^T)^{-1}, AA^+ = I$
→ right inverse matrix
1 2
x = np.array([[0,1],[1,-1],[-2,1]]) np.linalg.pinv(x) # 유사 역행렬 구하는 함수
np.linalg.pinv를 이용하면 데이터를 선형모델로 해석하는 선형 회귀식을 찾을 수 있다.
원래의 데이터 y와 우리가 예측한 y의 차이가 최소가 될 때 적절한 선형 모델을 찾았다고 할 수 있는데 이때 L2 norm을 최소화하는 베타를 찾으면 적절한 선형모델을 찾았다고 할 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12
# sklearn을 사용한 회귀 분석 y절편을 자동으로 추가해줌 from sklearn.linear_model import LinearRegression model = LinearRegression() # 모델 생성 model.fit(x,y) # 기울기 절편 계산 print(model.coef_) print(model.intercept_) y_test = model.predict(x_text) # Moore-Penrose 역행렬 X_ = np.array([np.append(x,[1]) for x in X]) # y절편 항을 추가해줘야함 beta = np.linalg.pinv(X_) @ y y_test = np.append(x,[1]) @ beta
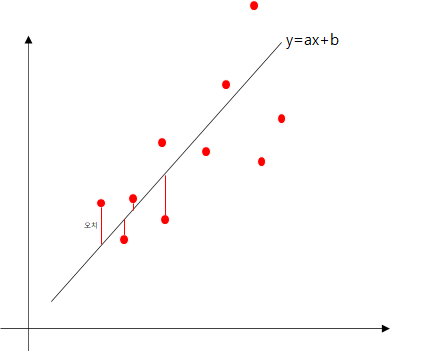
최소 제곱법
하나의 직선으로 표현할 수 없는 여러개의 데이터가 있을 때 특정 직선 $y = ax +b$ 를 만들어 점과 직선사이의 거리가 최소가 되도록 찾는 방법
![minima]()
이때 각 점(data)으로부터 직선까지의 모든 오차가 최소가 되도록 해야한다. 직선과 데이터의 위치에 따라 음수, 양수가 다르게 나올 수 있으므로 각 오차를 제곱하여 최소를 구한다(최소 제곱법).
모든 오차를 더한 E를 최소화 시켜야 하는데 E는 $||Ax - b||^2$ 으로 나타낼 수 있다.
$||Ax - b||^2$ 의 최소값을 구하는 것은 A의 Column Space와 b의 최단 거리를 구하는 것이다.
벡터공간 v에 속하는 벡터 중 x와 가장 가까운 것은 $proj_{v}x$ 이므로 우리는 $proj_{col(A)}b$ 를 구해야한다.
$Ax(최소) = proj_{col(A)}b = T(T^TT)^{-1}T^Tb$
($T = \begin{bmatrix}c_{1}&c_{2}\end{bmatrix}$, col(A)의 basis들을 열벡터로 하는 행렬)
위의 식으로 최소가 되는 Ax를 구하여 a,b값을 계산할 수 있다. 하지만 A가 full column rank(rank == column수)아닐 경우 위와 같은 식을 사용할 수 없다.
$Ax -y=proj_{col(A)}y - y$ 가 되는 순간 norm이 최소값이 된다.
$Ax -y=proj_{col(A)}y - y=-proj_{col(A)^ㅗ}y=-proj_{row(A^T)^ㅗ}y = -proj_{null(A^T)}y$
(참고 : $y =proj_{col(A)}y + proj_{col(A)^ㅗ}y$ )
위의 식을 보면 Ax-y가 $A^T$의 null space안에 있는 원소라는 뜻이 되므로
$A^T(Ax -y) = 0$이 되고,이 식을 전개하면 $A^TAx =A^Ty$가 되고 이 식을 정규 방정식이라고 한다. A가 full column rank라면 x를 $(A^TA)^{-1}A^Ty$로 해를 바로 구할 수 있고, full column rank가 아니라면 무수히 많은 해가 존재한다.
→하지만 의사 역행렬을 사용하면 해를 구할 수 있다.
- A가 full column rank일 경우 Ax=b의 최소 제곱 해는 $x =A^+b$
- A가 full column rank가 아닐 경우 x는 무수히 많은 해가 있지만 그 중 가장 norm이 짧은 해는 1번과 같다.