Keyword

Generalization

일반화란 학습데이터와 input data가 달라져도 성능 차이가 크게 나지 않도록 하는것을 말한다.

Generalization performance가 좋다는 것은 Train Error와 Test Error 차이가 적다는것을 말한다.

Under-fitting vs. over-fitting

모델이 너무 간단해 학습 오류가 줄어들지 않는 현상을 Under fitting, 학습 데이터의 오류는 작지만 테스트 데이터의 오류가 큰 경우를 Over fitting이라고 한다.

Cross validation

• 일반적인 Validation의 문제점

  일반적으로 Train set과 Test Set을 나누어 Train Data로 학습을 하고 Test Set으로 학습된 모델을 테스트한다. 이경우 학습을 시킬 때 Test Set만을 사용해 Validation하게 되고, 고정된 Test Set만을 사용해 Hyper Parameter를 수정하고, 학습하는 과정을 반복하게 되는데 이경우 고정된 Test Set에서만 잘 동작하는 모델이 나올 수 있다. 또는 고정된 Train Data를 사용하기 때문에 Train Data에 Over fitting될 수 있다.

• Cross Validation은 기존 Train Set에서 Validation Set을 지정해 매번 같은 Train Set과 Test Set을 사용하는것이 아닌 매번 다른 학습 데이터와 검증 데이터를 사용해 과적합을 줄이기 위해 사용된다. Hyper parameter튜닝을 위해서 사용되기도 한다.

• 종류

  다양한 교차 검증 방법이 존재한다.(https://en.wikipedia.org/wiki/Cross-validation_(statistics))

  1. K-Fold Cross validation
     • Train set을 k개의 Fold로 나누어 (k-1)개로 학습, 남은 하나의 fold로 validation을 수행하는 방법이다. validation set으로 사용되는 fold를 매번 바꾸면서 k번 반복 후 나온 결과를 평균내어 검증 결과로 사용한다.
     • 보통 k-fold는 일반화 성능을 만족시키는 최적의 hyper parameter를 선택할 때 사용된다. → ? Hyper Parameter 선택이 어떻게 이뤄지는거지…………
  2. Leave-p-out Cross validation
     • p개의 데이터를 추출해 validation set으로 사용하는 방법이다.
  3. Holdout Cross validation
     • train set을 임의의 비율로 다시 Train set 과 Test set(Validation Set)으로 분할해 사용하는 방법이다.
     • train set을 사용해 Validation Set에 대한 성능을 높이도록 학습하고, 기존 Test Set을 모델의 최종 성능을 추정하기 위해 사용한다.

Bias-variance tradeoff

• Variance는 비슷한 입력을 넣었을 때 출력이 얼마나 일관적인지를 나타낸다. Bias는 출력을 평균적으로 보았을 때 어떤 Target과 유사한지를 나타낸다.
• loss는 bias(편차), variance(분산), noise세개의 파트로 나누어 생각할 수 있다.

\[cost = 𝔼[(t-\hat{f})^2]=𝔼[(t-f+f-\hat{f})^2]\\=𝔼[(f-𝔼[\hat{f}^2])^2]+𝔼[(𝔼[\hat{f}-\hat{f)}^2]+𝔼[\epsilon]\\=bias^2+variance+noise\]

• bias, variance, noise의 3개의 term으로 나누어지는데 noise는 데이터의 태생적 한계이므로 어떤 모델을 사용하더라도 줄일 수 없다.
• 반면 bias와 variance는 모델에 따라 줄일 수 있는 reducible error이다.
• 이러한 분산과 편향을 모두 줄이는것이 가장 좋은 방법이지만 이 둘은 Trade off관계를 가진다.

Bootstrapping

학습데이터를 sub-sampling을 통해 여러개를 만들어 사용하는것을 의미

Ensemble(앙상블)

Ensemble학습은 여러개의 모델을 결합해 하나의 모델보다 더 좋은 성능을 내는 기법이다.

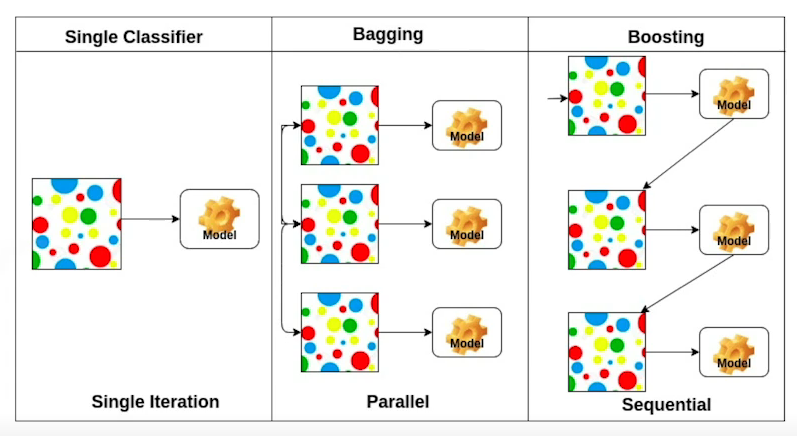
• Bagging(Bootstrapping aggregating)
  • 여러개의 모델을 Bootstrapping을 사용하여 학습하는것을 말한다.
  • sub-sampling을 통해 여러개의 Data를 만들고 여러 Model를 학습한 뒤 각 모델의 Output을 집계(Aggregration)하여 결과로 사용하는 방법이다.
  • Categorical Data의 경우 Voting으로 집계하고, Continuous Data는 평균으로 집계한다.
  • variance를 감소시킨다.
• Boosting
  • 여러개의 모델을 만들어 합치는것을 말한다.
  • 각각의 model을 Weak learner라고하고 이러한 Weak learner를 Sequential하게 합쳐 Structure learner를 만든다.
  • bias를 감소시킨다.

---

Gradient Descent

loss function을 업데이트 하고싶은 파라미터로 미분하여 나온 미분값으로 파라미터를 업데이트 하는 방식이다.

• stochastic gradient descent

  하나의 샘플을 사용해서만 gradient를 구해 파라미터를 업데이트

• Mini-batch gradient descent

  특정 batch size의 샘플을 사용해 gradient를 구해 파라미터를 업데이트

• Batch Gradient descent

  한번에 모든 데이터를 다 사용해 gradient를 구해 파라미터를 업데이트

---

Gradient Descent 최적화 알고리즘

$W_{t+1}\leftarrow W_{t}-\eta g_{t}$ Gradient Descent는 기존 파라미터에서 learning rate와 Gradient의 곱을 빼서 파라미터를 업데이트한다. learning rate를 어떻게 설정하느냐에 따라 큰 영향을 받게된다.

• Momentum
  • SGD에 관성이라는 개념을 추가한것이다.
  • 현재 Gradient를 통해 이동되는 방향만 고려하여 이동하는 것이 아니라 과거의 이동을 고려하여 업데이트 하는 방식이다.
  • $a_{t+1}\leftarrow \beta a_t + g_t$
  • $W_{t+1}\leftarrow W_{t}-\eta a_{t+1}$
  • $\eta$는 얼마나 momentum을 줄것인지를 나타낸다. (보통 0.9)
  • SGD의 경우 local minima에 빠질 경우 Gradient가 0이되어 이동할 수 없지만 Momentum의 경우 이전에 이동하려 했던 관성이 존재하기 때문에 탈출할 수 있다.
• Nesterov Accelerated Gradient(NAG)
  • Momentum은 관성과 현재 Gradient를 더하는것으로 update방향을 결정했지만 NAG는 Momentum만큼 이동했다고 가정한 뒤 Gradient를 구해 update방향을 결정한다.
  • $a_{t+1}\leftarrow\beta a_t+\nabla \mathcal{L}(W_t-\eta \beta a_t)$
  • $W_{t+1}\leftarrow W_t-\eta a_{t+1}$
• Adagrad
  • 고정된 learning rate를 사용하는것이 아닌 각 파라미터마다 적합한 learning rate를 가지도록 하는 방법이다.
  • 많이 변한 파라미터에 대해서는 더 적게 변화시키고 적게 변한 파라미터는 많이 변화시키는 방법이다.
  • 네트워크의 파라미터가 얼마나 변했는지에 따라 학습률을 점점 줄여간다고 생각하면된다.
  • $W_{t+1}\leftarrow W_t-\frac{\eta}{\sqrt{G_t+\epsilon}}g_t$
  • G는 지금까지 Gradient가 얼마나 많이 변했는지를 제곱해서 더한것이다
  • 문제점 : G가 계속 커지기 때문에 뒤로 갈수록 학습이 전혀 진행되지 않는다.
• Adadelta
  • Adagrad의 문제점을 보완하기위해 나온 방법이다.
  • G를 gradient의 제곱의 합이 아닌 제곱의 지수 평균으로 계산한다.
  • $G_t=\gamma G_{t-1}+(1-\gamma)g_t^2$
  • $W_{t+1} = W_t - \frac{\sqrt{H_{t-1} + \epsilon}}{\sqrt{G_t+\epsilon}}g_t$
  • $H_t=\gamma H_{t-1}+(1-\gamma)(\nabla W_t)^2$
• RMSprop(Root Mean Square Propagation)
  • 시간이 지남에 따라 극단적으로 Learning rate가 줄어드는 Adagrad를 보완한 방법이다.
  • G를 gradient의 제곱의 합이 아닌 제곱의 지수 평균으로 계산한다.
  • $G_t=\gamma G_{t-1}+(1-\gamma)g_t^2$
  • $W_{t+1} = W_t-\frac{\eta}{\sqrt{G_t+\epsilon}}g_t$
• Adam(Adaptive Moment Estimation)
  • Momentum과 AdaGrad의 기법을 모두 채용한 방법
  • 이전의 Gradient들을 통해 속도와, step size모두를 계산해 업데이트한다.
  • $\beta_1\beta_2\in[0,1]$은 hyper parameter이며 이동평균의 감쇠율을 조정한다.
  • $m_t,v_t$는 각각 경사의 평균과 분산의 추정값이다.
  • 4개의 파라미터를 정하는게 중요

---

Regularization(정규화)

Generalization성능을 높이는것을 Regularization이라한다.

• Early stopping
  • 학습을 멈추는것
  • 현재까지 학습된 모델의 성능을 Test Data를 사용해 평가해보고 loss가 커지기 시작하면 학습을 중지
• Parameter norm penalty
  • L1 Regularization (Lasso)
    • 기존 Cost function에 가중치의 절대값을 추가한 것이다.
    • 이러한 패널티로 매우 낮은 특성의 가중치를 정확히 0으로 유도해 모델에서 해당 특성을 배제할 수 있다.
  • L2 Regularization (Ridge)
    • 기존 Cost function에 가중치의 제곱을 추가한 것이다.
    • 높은 긍정값, 낮은 부정값을 가지는 이상점 가중치를 0에 가깝게 유도한다.
    • L1 Regularization과 다르게 정확히 0으로 유도하지는 못한다.
    • 선형모델의 일반화를 항상 개선한다.
• Data Augmentation
  • 데이터가 많으면 많을 수록 학습이 잘된다는 점을 이용해 주어진 데이터를 label에 벗어나지 않도록 적절히 변환 시키는것
• Noise Robustness
  • input과 weight에 noise를 넣기
• label smoothing
  • 분류문제의 label을 정확히 1과 0으로 두는것이 아니라 smooth하게 부여하는것을 말한다.
  • 이는 모델이 target을 정확하게 예측하지 않아도 되도록 만드는 방법
  • Mixup : 두개의 이미지를 골라 data와 label을 50:50으로 섞는다.
  • Cutout : 하나의 이미지에서 일정 영역을 잘라낸다.
  • Cutmix : 두개의 이미지를 섞는데 Mixup처럼 섞는것이 아닌 영역을 나누어 섞는다.
  • 분류문제에서 사용하면 노력대비 높은 성능 향상을 기대할 수 있다.
• Dropout
  • Forward Pass과정에서 랜덤하게 뉴런의 연결을 끊어버리는 방법이다.

  • 앙상블의 근사적인 방법이 될 수있다.

    뉴런을 끊는 작업으로 여러개의 서브 네트워크로 학습하는 것과 비슷하기때문

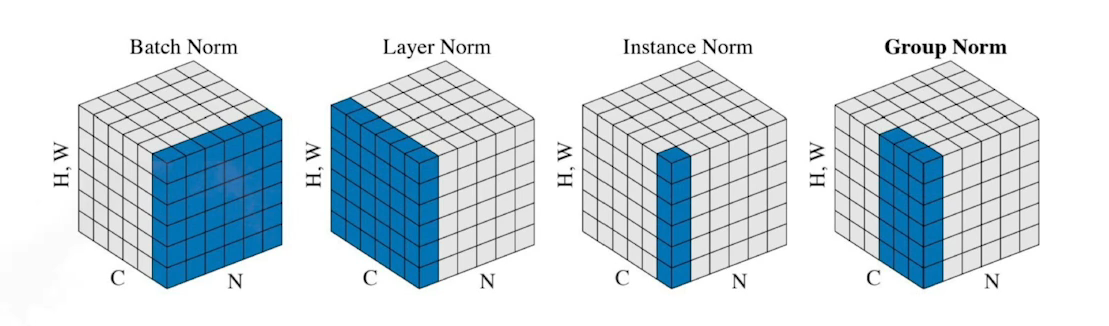
• Batch Normalization(?)
  • https://shuuki4.wordpress.com/2016/01/13/batch-normalization-설명-및-구현/